Here, you can find a (non-exhaustive!) list of the contents and take-aways of Chapter 5: Econometrics. This list serves as an opportunity to assess both how thoroughly you should read the chapter before opening it for the first time, and how well you have managed to follow along once you have read it.
Chapter 4: Econometrics introduces
-
- probability spaces and probability measures
- random variables and random vectors, their distribution and moments
- rules for working with expected values, variances and covariances
- the conditional expectation function
- different forms of convergence for series of random variables and limit theorems
- the linear regression model
Someone with profound knowledge of the contents of this chapter should
-
- understand what a marginal density is and how it relates to the joint density of two random variables
- be able to work with conditional probabilities and Bayes rule
- know that the conditional expectation function is itself a random variable
- be able to derive the OLS estimator as the solution to an unconstraint optimization problem, and from a moment condition
- be able to derive the asymptotic distribution of the OLS estimator using the Central Limit Theorem, the Weak Law of Large Numbers and Slutsky’s Theorem
- be able to work with some basic rules for conditional expectations
- know how the independence of two random variables is defined and what it implies for the covariance of these variables
- be able to derive rules for variances and covariances based on properties of the expected value, e.g. using its linearity
and be able to answer a number of related questions, including
-
- Why are OLS regressions important for economists?
- What is a probability measure?
- What does Convergence in Distribution imply for the cumulative distribution function of a series of random variables?
- What is the statement of the Central Limit Theorem? What is its role in Econometrics and Statistics?
- How is the conditional expectation function of a continuous random variable defined? How is it’s conditional density defined?
- What is the statement of Bayes’ Rule?
- Does the Weak Law of Large Numbers hold for random variables that have a finite expected value?
- Under which condition is the following true:
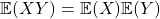 ?
?