Chapter 2 – Matrix Algebra – E600 Mathematics

An overview of this chapter’s contents and take-aways can be found here.

Table of Contents

Introduction

Very frequently as economists, we have to deal with matrices because they are at the heart of (constrained) optimization problems where we have more than one variable, e.g. utility maximization given budget sets, cost-efficient production given an output target with multiple goods or deviation minimization in statistical analysis when considering multiple parameters. To engage in such analysis, we need to know a variety of matrix properties, what operations we can apply to one or multiple matrices, and very importantly, how to use matrices to solve systems of linear equations.

When considering such systems, a number of (frequently non-obvious) questions are

1. Does a solution exist?
2. If so, is the solution unique? Otherwise, how many solutions are there?
3. How can we (or our computer) efficiently derive the (set of) solutions?

We will shortly define how matrices can be multiplied with each other and with vectors formally. For now, let us confine to the intuition of why matrices are a useful concept in the context of linear equation systems. Consider the system

$\begin{tabular}{rcrcrcc} $x_1$ & $+$ & $x_2$ & $+$ & $x_3$ & $=$ & $6$\\ & & $x_2$ & $-$ & $x_3$ & = & $0$\\ $5\cdot x_1$ & & & $+$ &$x_3$ &= &$1 $ \end{tabular}$

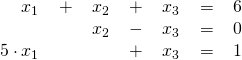
which, by stacking the equations into a vector, we can re-write as

$\begin{pmatrix} 1\cdot x_1 + 1\cdot x_2 + 1\cdot x_3\\ 0\cdot x_1 + 1\cdot x_2 + (-1)\cdot x_3 \\ 5\cdot x_1 + 0\cdot x_2 + 1\cdot x_3 \end{pmatrix} = \begin{pmatrix} 6 \\ 0 \\ 1\end{pmatrix} \hspace{0.5cm}\Leftrightarrow\hspace{0.5cm} Ax = \begin{pmatrix} 1 & 1 & 1\\ 0 & 1 & -1 \\ 5 & 0 & 1\end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \\ x_3\end{pmatrix} = \begin{pmatrix} 6 \\ 0 \\ 1\end{pmatrix} =: b$

where $x=(x_1,x_2,x_3)'$ and $A$ is the matrix on the LHS of the last equation. We will worry about why the equivalence holds after formally introducing matrix multiplication. Here, we see that generally, a system of $n$ equations in $k$ variables has a matrix representation with a coefficient matrix $A$ of dimension $n\times m$ and a solution vector $b\in\mathbb R^n$ . You may be familiar with a few characterizations of $A$ that help us to determine the number of solutions: In many cases, if $n\geq k$ , we can find at least one vector $x$ that solves the system, and if $n>k$ , then there are generally infinitely many solutions. However, there is much more we can say about the solutions from looking at $A$ , and how exactly this works will be an central aspect of this chapter.

Basics and the Matrix Vector Space

Because we want to do mathematical analysis with matrices, a first crucial step is to make ourselves aware of the algebraic structure that we attribute to a set of matrices with given dimensions that allow to perform mathematical basis operations (addition and scalar multiplication), that serve as ground for any further analysis we will eventually engage in. As a first step, let us formally consider what a matrix is:

Definition: Matrix of dimension $n\times m$ .
Let $(a_{ij}: i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\})$ be a collection of elements from a basis set $X$ , i.e. $\forall i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}:a_{ij}\in X$ . Then, the matrix $A$ of these elements is the ordered two-dimensional collection

$A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nm} \end{pmatrix}.$

We call $n$ the row dimension of $A$ and $m$ the column dimension of $A$ . We write $A\in X^{n\times m}$ . As an alternative notation, one may write $A = (a_{ij})_{i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}}$ , or, if $n=m$ , $A = (a_{ij})_{i,j\in\{1,\ldots,n\}}$ .

In the following, we restrict attention to $X=\mathbb R$ , so that the $a_{ij}$ are real numbers. Note however that this need not be the case; indeed, an important concept in econometrics are so-called block-matrices $A= (A_{ij})_{i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}}$ where the $A_{ij}$ are matrices of real numbers, and for derivatives, we frequently consider matrices of (derivative) operators, that is, functions, as opposed to numbers. Moreover, the entries can be random variables (in econometrics), functions, and even operators, as we will see in chapter 3.

To apply the vector space concept to matrices, note that matrices of real numbers can be viewed as a generalization of real vectors: a vector $x\in\mathbb R^n$ is simply a matrix of dimension $n\times 1$ . We now consider objects that may have multiple columns, or respectively, stack multiple vectors in an ordered fashion. Thus, when $a_1,\ldots, a_k\in\mathbb R^n$ are the columns of a matrix $A\in\mathbb R^{n\times m}$ , we may also write $A = (a_1, a_2,\ldots, a_k)$ (an alternative, yet less frequently used notation stacks the rows of $A$ on top of each other). Therefore, a natural way of defining addition and scalar multiplication for matrices is to apply the operators of the real vector context “element”-wise, i.e. for each column separately:

Definition: Addition of Matrices.
For two matrices $A$ and $B$ of identical dimension, i.e. $A = (a_{i,j})_{i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}}$ and $B = (b_{i,j})_{i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}}$ , their sum is obtained from addition of their elements, that is

$A+B=(a_{i,j}+b_{i,j})_{i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}}.$

Note that to conveniently define addition, we have to restrict attention to matrices of the same dimension! This already means that we will consider not the whole universe of matrices as a vector space, but each potential specific combination of dimensions separately.

Definition: Scalar Multiplication of Matrices.
Let $A = (a_{i,j})_{i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}}$ and $\lambda \in \mathbb{R}$ . Then, scalar multiplication of $A$ with $\lambda$ is defined element-wise, that is

$\lambda A := (\lambda a_{i,j})_{i=1,...,n,j=1,...,m}.$

From chapter 1, we know that for graphical and also formal intuition, it is very useful if some algebraic structure constitutes a vector space, because then, we can deal with it very “similar” to the way we work with real numbers. Indeed, the set of matrices of given dimensions $n\times m$ , together with addition and scalar multiplication as we just defined, constitutes a real vector space:

Theorem: Vector Space of Matrices.
The set of all $n \times m$ matrices, $M_{n \times m}$ together with the algebraic operations matrix addition and multiplication with a scalar as defined above defines a vector space.

While we will not be concerned much with distances of matrices in this course, defining them in accordance with the previous chapter is indeed possible: the matrix norm commonly used is very similar to the maximum-norm defined earlier:

$\| A\|_{\infty} = \max\{|a_{ij}|: i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}\}.$

Should you be curious or feel that you need some more practice with the norm concept, you can try to verify that this indeed constitutes a norm, checking all 3 parts of the norm definition.

Important Matrices

Before we move to deeper analysis of matrices and their usefulness for the purpose of the economist, some review and introduction of important vocabulary is necessary. In this section, you can find a collection of the most central terminology for certain special characteristics matrices may have.

First, when characterizing matrices, it may be worthwhile to think about when we say that two matrices are equal.

Definition: Matrix Equality.
The matrices $A = (a_{ij})_{i\in\{1,\ldots,n\},j\in\{1,\ldots,m\}}$ and $B= (b_{ij})_{i\in\{1,\ldots,r\},j\in\{1,\ldots,s\}}$ are said to be equal if and only if (i) they have the same dimension, i.e. $(n=r\land m=s)$ , and (ii) all their elements are equal, i.e. $\forall i\in\{1,\ldots,n\},j\in\{1,\ldots,m\}: a_{ij} = b_{ij}$ .

Note especially that it is thus not sufficient that e.g. all elements equal the same value, so that the matrices $\mathbf 0_{2\times 2} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$ and $\mathbf 0_{2\times 3} = \begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}$ are not equal.

Definition: Transposed Matrix.
Let $A = (a_{ij})_{i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}}\in\mathbb R^{n\times m}$ . Then, the transpose of $A$ is the matrix $A' = (a'_{ij})_{i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}} \in\mathbb R^{m\times n}$ where $\forall i\in\{1,\ldots,n\}, j\in\{1,\ldots,m\}$ , $a'_{ij} = a_{ji}$ . Alternative notations are $A^T$ or $A^t$ .

Thus, the transpose $A'$ “inverts” the dimensions, or respectively, it stacks the columns of $A$ in its rows (or equivalently, the rows of $A$ in its columns). Note that dimensions “flip”, i.e. that if $A$ is of dimension $n\times m$ , then $A'$ is of dimension $m\times n$ . An example is given below in equation (1).

Definition: Row and Column Vectors.
Let $A\in\mathbb R^{n\times m}$ . If $n=1$ , $A$ is called a row vector, and a column vector if $m=1$ . By convention, one also calls a column vector simply vector.

According to this definition, as we also did before with vectors in $\mathbb R^n$ , when you just read the word “vector”, you should think of a column vector.

Definition: Zero Matrices.
The zero matrix of dimension $n \times m$ , denoted $\mathbf{0}_{n \times m}$ , is the $n \times m$ matrix where every entry is equal to zero.

Definition: Square Matrix.
Let $A\in\mathbb R^{n\times m}$ . Then, if $n=m$ , $A$ is said to be a square matrix.

Definition: Diagonal Matrix.
A square matrix $A = (a_{ij})_{i,j\in\{1,\ldots,n\}}\in\mathbb R^{n\times n}$ is said to be a diagonal matrix if all of its off-diagonal elements are zero, i.e. $(i\neq j\Rightarrow a_{ij} = 0)$ . We write $A = \text{diag}\{a_{11},\ldots,a_{nn}\}$ .

Note that the diagonal elements $a_{ii}$ , $i\in\{1,\ldots,n\}$ need not be non-zero for $A$ to be labeled “diagonal”, and thus, e.g. the zero matrix is diagonal, and so is $A = \begin{pmatrix} 1 & 0 \\ 0 & 0\end{pmatrix}$ .

Definition: Upper and Lower Triangular Matrix.
A square matrix $A = (a_{ij})_{i,j\in\{1,\ldots,n\}}\in\mathbb R^{n\times n}$ is said to be upper triangular if $(i>j\Rightarrow a_{ij}=0)$ , i.e. when the entry $a_{ij}$ equals zero whenever it lies below the diagonal. Conversely, $A$ is said to be lower triangular if $A'$ is upper triangular, i.e. $(i<j\Rightarrow a_{ij}=0)$ .

Rather than studying the definition, the concept may be more straightforward to grasp by just looking at an upper triangular matrix:

(1) $\begin{equation*} A = \begin{pmatrix} 1&2&3&4\\ 0&1&1&0\\ 0&0&-4&3\\ 0&0&0&2\end{pmatrix} \wspace{\text{for which}} A' = \begin{pmatrix} 1&0&0&0\\ 2&1&0&0\\ 3&1&-4&0\\ 4&0&3&2\end{pmatrix}. \end{equation*}$

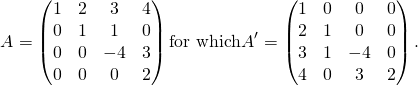
From its transpose, you can see why the transposition concept is used in the definition for the lower triangular matrix.

Definition: Symmetric Matrix.
A square matrix $A = (a_{ij})_{i,j\in\{1,\ldots,n\}}\in\mathbb R^{n\times n}$ is said to be symmetric if $\forall i,j\in\{1,\ldots,n\}: a_{ij} = a_{ji}$ .

Equivalently, symmetry is characterized by coincidence of $A$ and its transpose $A'$ , i.e. $A=A'$ .

Definition: Identity Matrices.
The $n \times n$ identity matrix, denoted $\mathbf{I_n}$ , is a diagonal matrix with all its diagonal elements equal to 1.

Again, the concept may be more quickly grasped visually:

$\mathbf{I_n} = \begin{pmatrix} 1&0&\cdots&0\\ 0&1&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\cdots&0&1\end{pmatrix}.$

To check your understanding and to get more familiar with the concepts, think about the following questions:

1. Consider a three-by-three matrix where the (2,2)-entry is equal to one, and all other entries are zero. Is this matrix
  1. lower triangular?
  2. diagonal?
  3. an identity matrix?
  4. square?
2. Can a lower triangular matrix have strictly more rows than columns?
3. True or false: A matrix is diagonal if and only if it is both upper triangular and lower triangular.

1: yes – yes – no – yes, 2. no, 3. true

Fundamentals of Calculus with Matrices

Now that we have laid the formal foundation by introducing the vector spaces of matrices of certain dimension and made ourselves familiar with a variety of important matrices, it is time to take a closer look on how we do calculus with matrices beyond the basis operations. Similar to the scalar product discussed for vectors, we first should know how to multiply two elements of the vector space with each other, rather than just one element with a scalar:

Definition: Matrix Product.
Consider two matrices $A\in\mathbb R^{n\times m}$ and $B\in\mathbb R^{m\times k}$ so that the column dimension of $A$ is equal to the row dimension of $B$ . Then, the matrix $C \in\mathbb R^{n\times k}$ of column dimension equal to the one of $A$ and row dimension equal to the one of $B$ is called the product of $A$ and $B$ , denoted $C= A\cdot B$ , if $\forall i\in\{1,\ldots,n\}, j\in\{1,\ldots,k\}: c_{ij} = \sum_{l=1}^m a_{il}b_{lj}$ .

As made clear by the bold text, matrix multiplication is subject to a compatibility condition, that differs from the one discussed before for addition. Thus, not all matrices that can be multiplied with each other can also be added, and the converse is also true.

To see just how closely this concept relates to the scalar product, write $A$ in row notation and $B$ in column notation, i.e. let $a_1,\ldots,a_n\in\mathbb R^{1\times m}$ be row vectors such that 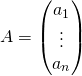$A = \begin{pmatrix} a_1\\\vdots\\a_n \end{pmatrix}$ and $b_1,\ldots,b_k\in\mathbb R^m$ column vectors so that $B = \begin{pmatrix} b_1&\cdots&b_k \end{pmatrix}$ . Then,

$AB = \begin{pmatrix}a_1'\cdot b_1 &a_1'\cdot b_2 & \cdots & a_1'\cdot b_k \\ a_2'\cdot b_1 &a_2'\cdot b_2 & \ddots & \vdots \\ \vdots & \ddots & \ddots & a_{n-1}'\cdot b_k \\ a_n'\cdot b_1 & \cdots & a_n'\cdot b_{k-1} & a_n'\cdot b_k, \end{pmatrix}$

and the matrix product emerges just as an ordered collection of the scalar products of $A$ ‘s rows with $B$ ‘s columns!

It may require some practice to confidently handle matrix multiplication, but if you aren’t already, you should become familiar with it rather quickly. Here is an example that visually illustrates how the entries in the matrix product come to be:

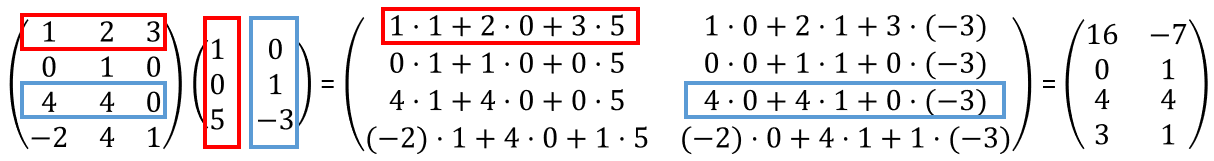
If you try to multiply this expression the other way round, you will quickly see that this doesn’t work: recall that the “inner” dimensions needed to coincide, so if $A$ is $n\times \underline{k}$ , $B$ must be $\underline{k}\times m$ for the product to exist. Thus, $AB$ and $BA$ exist if and only if the matrices are square and of equal dimension! And even then, it will generally not hold that $AB = BA$ .

Besides its complicated look, matrix multiplication does have some desirable properties:

Theorem: Associativity and Distributivity of the Product.
Assuming that $A,B,C$ are matrices of appropriate dimension, the product for matrices is

1. Associative: $(AB)C=A(BC)$
2. Distributive over matrix addition: $A(B+C) = AB+AC$ and $(A+B)C = AC+BC$

In terms of computing a matrix product, this especially means that the order in which you multiply matrices with each other does not matter. The theorem tells us that standard rules related to addition and multiplication continue to hold for matrices, e.g. when $A,B,C$ and $D$ are matrices of appropriate dimension, then $(A+B)(C+D)=AC+BC+AD+BD$ . An exception is of course that, as discussed above, commutativity of multiplication is not guaranteed.

It is noteworthy that the zero and identity element in the matrix space can be dealt with in a fashion very similar to the numbers 0 and 1 in $\mathbb R$ :

Theorem: Zero and Identity matrix.
Let $A\in\mathbb R^{n \times m}$ . Then,

1. $A + \mathbf{0}_{n\times m} = A$ .
2. For any $k\in\mathbb N$ , $A \cdot \mathbf{0}_{m\times k} = \mathbf{0}_{n\times k}$ and $\mathbf{0}_{k\times n}\cdot A = \mathbf{0}_{k\times m}$ .
3. For any $k\in\mathbb N$ , $A \cdot \mathbf{I_m} = A$ and $\mathbf{I_n}\cdot A = A$ .

Be sure to carefully think about where the dimensions of the zero and identity matrices come from, i.e. why they are chosen like this in the theorem! From this, take away that zero and identity matrix work in the way you would expect them to, and that there are no extraordinary features to be taken into account. Further useful properties of matrix operations are

Theorem: Transposition, Sum, and Product.

1. Let $A,B\in\mathbb R^{n \times m}$ . Then,
  $(A+B)^{\prime}=A^{\prime}+B^{\prime}$
2. Let $A\in\mathbb R^{n \times m}$ , $B\in\mathbb R^{m \times k}$ . Then:
  $(AB)^{\prime}={B}^{\prime}{A}^{\prime}$
3. If $A\in\mathbb R^{1 \times 1}$ , then $A$ is actually a scalar and $A^{\prime}=A$ .

While the former two points are more or less obviously useful, the third may appear odd; isn’t this obvious?! Why should it be part of a theorem? Well, the practical use is that frequently, this can be used to achieve a more convenient representation of complex expressions. For instance, in econometrics, when $\beta$ denotes a vector of linear regression model coefficients (if you are not familiar with this expression, it’s not too important what precisely this quantity is right now, just note that $\beta\in\mathbb{R}^{k+1}$ , where $k$ is the number of model variables), the squared errors in the model $y_i = x_i'\beta + u_i$ ( $y_i$ random variable, $x_i$ random vector of length $k+1$ ) that are of interest to estimator choice are

$u_i^2 = (y_i - x_i'\beta)^2 = y_i^2 - 2y_ix_i'\beta + (x_i'\beta)^2.$

Now, when taking expectations of such an expression (summand-wise), we want the non-random parameters (here: $\beta$ ) to either be at the beginning or the end of an expression. For the last one, this is not immediately the case: $(x_i'\beta)^2 = x_i'\beta\cdot x_i'\beta$ . However, noting that $x_i'\beta$ is scalar, $x_i'\beta = (x_i'\beta)' = \beta'x_i$ (with Point 2. in the Theorem), and thus, $(x_i'\beta)^2 = \beta'x_i x_i'\beta$ , an expression that we can handle well also when considering the expected value.

As a final remark on notation, note that we can use matrices (and vectors as special examples of them) for more compact representations. Consider the problem of estimating the parameter $\beta$ that we just considered above. Here, our standard go-to choice is the ordinary least squares (OLS) estimator $\hat\beta$ , which minimizes the sum of squared residuals in prediction of $y_i$ using the information $x_i$ and the prediction vector $b$ over all possible prediction vectors $b$ ‘s:

$SSR(b) = \sum_{i=1}^n (y_i - x_i'b)^2 = \sum_{i=1}^n u_i(b)^2.$

When defining $u(b) = (u_1(b),\ldots,u_n(b))'$ , we can simply write $SSR(b) = u(b)'u(b)$ . Generally, note that the scalar product of a vector with itself is just the sum of squares:

$\forall v=(v_1,\ldots,v_n)'\in\mathbb R^n: v'v=\sum_{j=1}^nv_j^2.$

Similarly, this applies to sums of matrices and sums of vector products.

This concludes our introductory discussion of matrices and matrix algebra. If you feel like testing your understanding of the concepts discussed thus far, you can take a short quiz found here.

Matrices and Systems of Linear Equations

Re-consider the system of linear equations discussed earlier in this chapter. Here, you saw that stacking the equations into a vector, one could arrive at a matrix representation with just one equality sign, characterized by

(2) $\begin{equation*} Ax = b, \end{equation*}$

where $A$ is a matrix of LHS coefficients of the variables $x_1,\ldots, x_n$ stacked in $x$ , and $b$ is the vector of RHS “result” coefficients. In the case of the example above, the specific system is

$\underbrace{\begin{pmatrix} 1 & 1 & 1\\ 0 & 1 & -1 \\ 5 & 0 & 1\end{pmatrix}}_{=A}\underbrace{\begin{pmatrix} x_1 \\ x_2 \\ x_3\end{pmatrix}}_{=x} = \underbrace{\begin{pmatrix} 6 \\ 0 \\ 1\end{pmatrix}}_{=b}.$

As an exercise of how matrix multiplication works, you can multiply out $Ax$ in this example and verify that $Ax=b$ is indeed equivalent to the system of individual equations.

Recall that our central questions to this equation system were:

1. Does a solution exist?
2. If so, is the solution unique? Otherwise, how many solutions are there?
3. How can we (or our computer) efficiently derive the (set of) solutions?

Thus, the issue at hand is to characterize the solution(s) for $x$ , i.e. the vectors $x\in\mathbb R^n$ that satisfy equation (2), ideally in a computationally tractable way.

As always, let us get an intuition for the things we don’t know starting from something we know: if $A, x$ and $b$ were real numbers and $A$ was unequal to zero, you immediately know how to solve for $x$ : just bring $A$ to the other side by dividing by it. If instead $A=0$ (i.e. $A$ can not be “inverted”), you know that there is no solution for $x$ if $b\neq 0$ , but if $b = 0$ , there are a great variety of solutions for $x$ — indeed, every $x\in\mathbb R$ would solve the equation. The idea is very similar with matrix equations, we just need a slightly different or respectively more general notion of “dividing by” and “invertibility”.

Similar to calculus with real numbers, we can define a multiplicative inverse for some $A\in\mathbb R^{n\times n}$ :

Definition: Inverse Matrices.
Consider two invertible square matrices $A,M\in\mathbb R^{n\times n}$ . Then, $M$ is called the inverse of $A$ if $MA = AM = \mathbf{I_n}$ . We write $M = A^{-1}$ so that $A^{-1}A = A A^{-1} = \mathbf{I_n}$ .

As with real numbers, we can show that the multiplicative inverse is unique, i.e. that for every $A\in\mathbb R^{n\times n}$ , there exists at most one inverse matrix $A^{-1}$ :

Proposition: Uniqueness of the Inverse Matrix.
Let $A\in\mathbb R^{n\times n}$ and suppose that the inverse of $A$ exists. Then, the inverse of $A$ is unique.

However, existence is not guaranteed, and in contrast to the real numbers, more than a single element ( $0$ ) will be non-invertible in the space $R^{n\times n}$ . Existence of the inverse is rigorously discussed below. For now, you should take away that the easiest case of a system of linear equations is one where the matrix $A$ is invertible. Indeed, the following sufficient condition is what economists rely on most of the time when solving linear equation systems:

Proposition: Invertibility of Unique Solution Existence.
Consider a system of linear equations $Ax = b$ with unknowns $x\in\mathbb R^n$ and coefficients $A\in\mathbb R^{m\times n}$ , $b\in\mathbb R^n$ . Then, if $m=n$ and $A$ is invertible, the system has a unique solution given by $x^* = A^{-1}b$ .

To see this, suppose $A$ is invertible, and that $x^*\in\mathbb R^n$ solves the system. Then,

$b = Ax^* \hspace{0.5cm}\Leftrightarrow\hspace{0.5cm} A^{-1}b = A^{-1}Ax^* = \mathbf{I_n} x^* = x^*.$

As discussed above, if we can invert $A$ , we can just bring it to the other side, this is exactly the same principle as with a single equation with real numbers. For this sufficient condition to be applicable, we must have that $m=n$ for $A$ to be square, i.e. we must have as many equations as unknowns. It may also be worthwhile to keep in mind that the converse of the Proposition above is also true: If $Ax=b$ has a unique solution and $A$ is square, then $A$ is invertible.

Invertibility of Matrices

While we have just seen the value of the inverse matrix in solving linear equation systems, we do not yet know how we determine whether $A$ can be inverted and if so, how to determine the inverse — so let us focus on these issues now.

First, some helpful relationships for inverse matrices are:

Proposition: Invertibility of Derived Matrices.
Suppose that $A,B\in\mathbb R^{n\times n}$ are invertible. Then,

- $A'$ is invertible and $(A')^{-1} = (A^{-1})'$ ,
- $AB$ is invertible and $(AB)^{-1} = B^{-1}A^{-1}$ ,
- $\forall \lambda\in\mathbb R$ , $\lambda\neq 0$ , $\lambda A$ is invertible and $(\lambda A)^{-1} = 1/\lambda A^{-1}$ .

To get more familiar with inverse matrices, let us briefly consider why this proposition is true:

For the first point, note that $\mathbf{I_n}' = \mathbf{I_n}$ . Thus,

$AA^{-1} = \mathbf{I_n} \hspace{0.5cm}\Leftrightarrow\hspace{0.5cm} \mathbf{I_n} = (AA^{-1})' = (A^{-1})' A'.$

Therefore, $(A^{-1})'$ is the inverse matrix of $A'$ .

For the second point, by associativity of the matrix product,

$[B^{-1} A^{-1}]\cdot AB = B^{-1}\underbrace{(A^{-1} A)}_{=\mathbf{I_n}}B = B^{-1} B = \mathbf{I_n}.$

For the third, for any $\lambda\in\mathbb R$ , $\lambda\neq 0$ is a $1\times 1$ matrix, and we know that it is invertible with $\lambda^{-1} = 1/\lambda$ . Thus, the third point is a direct implication of the second.

An important corollary is obtained by iterating on the second point:

Corollary: Invertibility of Long Matrix Products.
For any $p\in\mathbb N$ , if $A_1,\ldots, A_p\in\mathbb R^{n\times n}$ are invertible, then $A_1\cdot\ldots\cdot A_p$ is invertible with inverse $(A_1\cdot\ldots\cdot A_p)^{-1} = A_p^{-1} \cdot A_{p-1}^{-1}\cdot\ldots\cdot A_1^{-1}$ .

While this proposition and its corollary are very helpful, they still assume invertibility of some initial matrices, and therefore do not fundamentally solve the “when-and-how” problem of matrix inversion. In this course, we first focus on the “when”, i.e. the conditions under which matrices can be inverted. Here, there are four common possible approaches: the determinant, the rank, the eigenvalues and the definiteness of the matrix.

Before introducing and discussing these concepts, it is instructive to make oneself familiar with the elementary operations for matrices. Not only are they at the heart of solving systems of linear equations, but they also interact closely with all concepts discussed next.

Elementary Matrix Operations

Let’s begin with the definition:

Definition: Elementary Matrix Operations.
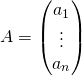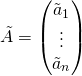For a given matrix $A = \begin{pmatrix}a_1\\\vdots\\a_n\end{pmatrix}$ with rows $a_1',\ldots,a_n'\in\mathbb R^n$ , consider an operation on $A$ that changes the matrix to $\tilde A$ , i.e. $A\rightarrow \tilde A$ where $\tilde A = \begin{pmatrix}\tilde a_1\\\vdots\\\tilde a_n\end{pmatrix}$ . The three elementary matrix operations are

- (E1) Interchange of two rows $i,j$ : $\tilde a_i = a_j$ , $\tilde a_j = a_i$ and $\tilde a_k = a_k$ for all $k\notin\{i,j\}$ ,
- (E2) Multiplication of a row $i$ with a scalar $\lambda\neq 0$ : $\tilde a_i = \lambda a_i$ and $\tilde a_j = a_j$ for all $j\neq i$ ,
- (E3) Addition of a multiple of row $j$ to row $i$ : $\tilde a_i = a_i + \lambda a_j$ , $\lambda\in\mathbb R$ , and $\tilde a_j = a_j$ for all $j\neq i$ .

To increase tractability of what we do, the following is very helpful:

Proposition: Matrix Representation of Elementary Operations.
Every elementary operation on a matrix $A\in\mathbb R^{n\times m}$ can be expressed as left-multiplication a square matrix $E\in\mathbb R^{n\times n}$ to $A$ .

- (E1) The exchange of rows $i$ and $j$ is represented by $E^1 = (e^1_{kl})_{k,l\in\{1,\ldots,m\}}$ with $e^1_{ij} = e^1_{ji} = 1$ , $e^1_{kk} = 1$ for all $k\notin\{i,j\}$ and $e^1_{kl}=0$ else.
- (E2) Multiplication of a row $i$ with $\lambda\neq 0$ is represented by the diagonal matrix $E^2 = (e^2_{kl})_{k,l\in\{1,\ldots,m\}}$ where $e^2_{kl} = 0$ for any $k\neq l$ (the definition of a diagonal matrix), $e^2_{ii} = \lambda$ and $e^2_{jj} = 1$ for $j\neq i$ .
- (E3) Addition of a multiple $\lambda\in\mathbb R$ of row $j$ to row $i$ is represented by the triangular matrix $E^3 = (e^3_{kl})_{k,l\in\{1,\ldots,m\}}$ with $e^3_{kk} = 1$ for all $k\in\{1,\ldots, m\}$ and $e^3_{ij} = \lambda$ .

To see these rather abstract characterizations in a specific example, consider a system with 4 rows and suppose that we use (E1) to exchange rows 1 and 3, (E2) to multiply the fourth row by 5 and (E3) to add row 2, multiplied by 2, to row 3. Then, the associated matrices are

$E^1 = \begin{pmatrix} 0 & 0 & 1 & 0\\ 0&1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}, \hspace{0.5cm}\Leftrightarrow\hspace{0.5cm} E^2 = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0&1 & 0 & 0\\0 & 0 & 1 & 0\\ 0 & 0 & 0 & 5 \end{pmatrix}, \hspace{0.5cm}\Leftrightarrow\hspace{0.5cm} E^3 = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0&1 & 0 & 0\\0 & 2 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}.$

If you have some time to spare, it may be a good exercise to come up with some examples and verify that this matrix-approach indeed does what we want it to do.

As stated above, the practical value of this proposition lies in the fact that when we bring a matrix $A$ to another matrix $\tilde A$ using the elementary operations $E_1,\ldots, E_k$ , where the index $j$ of $E_j$ indicates that $E_j$ was the $j$ -th operation applied, then we can write

$\tilde A = E_k\cdot E_{k-1}\cdot\ldots\cdot E_{1}A.$

This increases tractability of the process of going from $A$ to $\tilde A$ , a fact which we will repeatedly exploit below.

The key feature of the elementary operations is that one may use them to bring any square matrix to upper triangular form as defined in the previous section (more generally, any arbitrary matrix can be brought to a “generalized” upper triangular form – since we only deal with square matrices here, we need not bother too much with this result, though):

Theorem: Triangulizability of a Matrix.
Consider a matrix $A\in\mathbb R^{n\times m}$ . Then, if $n=m$ , $A$ can be brought to upper triangular form applying only elementary operations to $A$ .

This is helpful because, as will emerge, both the determinant and rank invertibility condition hold for an initial matrix if and only if they hold for an upper triangular matrix obtained from applying elementary operations to $A$ . You can find the details of why this theorem applies in the companion script. For now, it is enough to know that this works. How a given matrix can be triangularized will be studied once we turn to the Gauss-Jordan algorithm, our go-to procedure that we use for matrix inversion.

So, how do elementary operations help us when thinking about the inverse of a matrix? The connection is stunningly simple: suppose that we can bring a square $n\times n$ matrix $A$ not only to triangular, but diagonal form with an all non-zero diagonal using the operations $E_1,\ldots,E_k$ , i.e.

$E_k\cdot\ldots\cdot E_1 A = \begin{pmatrix} \lambda_1 & 0 & \cdots & 0\\ 0 & \lambda_2 & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & \lambda_k\end{pmatrix} = \text{diag}\{\lambda_1,\ldots,\lambda_n\}$

where $\forall j\in\{1,\ldots,n\}: \lambda_{j}\neq 0$ . Then, multiplying all columns $j$ by $1/\lambda_j$ , summarized by $E_{k+1} = \text{diag}\{1/\lambda_1,\ldots,1/\lambda_n\}$ , with $E := E_{k+1}\cdot E_k\cdot\ldots\cdot E_1$ , one has $EA = \mathbf{I_n}$ . This is very convenient: the transformation matrix $E$ is precisely what we call the inverse matrix of $A$ , i.e. $E = A^{-1}$ ! Thus, we can summarize the following:

Proposition: Invertibility and Identity Transformation.
If we can use elementary operations $E_1,\ldots,E_k$ to bring a matrix $A\in\mathbb R^{n\times n}$ to the identity matrix, then $A$ is invertible with inverse $A^{-1} = E$ where $E:= E_k\cdot\ldots\cdot E_1$ .

Indeed, we will see later that the converse is also true. As you will see in the last section, the ensuing result is what we base upon our method of computing inverse matrices, the Gauß-Jordan algorithm: to compute the matrix $E$ , note that $E = E\cdot \mathbf{I_n}$ , so that when bringing an invertible matrix $A$ to identity form, we just have to apply the same operations in the same order to the identity matrix to arrive at the inverse! Don’t worry if this sounds technical, it’s not, hopefully, the examples we will see later will convince you of this.

Before moving on, let us briefly consider why we cared about the upper triangular matrix in the first place – after all, it is the diagonal matrix with the $\lambda$ ‘s that we want, isn’t it?! Well, the thing is, once we arrive at the triangular matrix we are basically done: suppose that, starting from some arbitrary matrix $A$ , we have arrived at the triangular matrix

$\begin{pmatrix} 2 & 9 & 3\\ 0 & 4 & -2\\ 0 & 0 & 5 \end{pmatrix}.$

Then, multiplying the last row with $1/5$ and subsequently adding (1) $2$ times the last row to row 2 and (2) $-3$ times the last row to row 1 gives

$\begin{pmatrix} 2 & 9 & 0\\ 0 & 4 & 0\\ 0 & 0 & 1 \end{pmatrix}.$

Next, multiplying the second row with $1/4$ and subsequently adding it $-9$ times to the first gives the desired diagonal. With a bit more technicality and notation, this line of reasoning generalizes to upper triangular matrices of any dimension.

Thus, we can summarize: If a matrix can be brought to upper triangular form with an all non-zero diagonal using elementary operations, it can also be brought to the identity matrix using elementary operations, and therefore inverted. Because any matrix can be triangularized, we can test invertability by checking if the associated triangular form has zeros on the diagonal.

Determinant of a Square Matrix

Now, it is time to turn to our most common matrix invertibility check, the determinant. The very first thing to note about the determinant concept is that ONLY square matrices have a determinant!, i.e. that for any non-square matrix, this quantity is NOT defined!

To give some intuition on the determinant, it may be viewed as a kind of “matrix magnitude” coefficient similar to the one we studied in the vector case, which augments a vector’s directionality. This intuition is helpful because it turns out that as with real numbers, we can invert anything that is of non-zero magnitude — i.e. any matrix with non-zero determinant! However, note that unlike with a vector, a matrix with non-zero entries can have a zero determinant and thus have “zero magnitude”, so that this reasoning should be viewed with some caution.

The general definition of the determinant is unnecessarily complex for our purposes. We will define the determinant recursively here, that is, we first define it for simple $1 \times 1$ matrices, and then express the determinant of an $n \times n$ matrix as a function of that of several $(n-1) \times (n-1)$ matrices, which each can be expressed with the help of determinants of $(n-2) \times (n-2)$ matrices, and so on. It is conceptually more straightforward and sufficient for the use you will make of them.

Definition: Determinant.
Let $A\in\mathbb R^{n\times n}$ . Then, for the determinant of $A$ , denoted $\det(A)$ or $|A|$ , we define

if $n=1$ and $A = (a)$ is a scalar, $\det (A) = \det (a) := a$ .
for all $n\in\mathbb N: n\geq 2$ , when
$A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} &\cdots & a_{nn}\end{pmatrix},$

$\det(A) := \sum_{j=1}^n (-1)^{i+j}a_{ij}\det(A_{-ij})$ with $i=1$ and $A_{-ij}$ as the matrix resulting from eliminating row $i$ and column $j$ from $A$ , i.e.

$A_{-ij} = \begin{pmatrix} a_{11} & \cdots & a_{1,j-1} & a_{1,j+1}&\cdots & a_{1n}\\ \vdots & & \vdots & \vdots &&\vdots\\ a_{i-1,1} & \cdots & a_{i-1,j-1} & a_{i-1,j+1}&\cdots & a_{i-1,n}\\ a_{i+1,1} & \cdots & a_{i+1,j-1} & a_{i+1,j+1}&\cdots & a_{i+1,n}\\ \vdots & & \vdots & \vdots &&\vdots\\ a_{n1} & \cdots & a_{n,j-1} & a_{n,j+1}&\cdots & a_{nn}\\ \end{pmatrix}.$

This definition allows to obtain the determinant for any arbitrary $n\times n$ matrix by decomposing the $A_{-ij}$ ‘s into smaller matrices until we have just $1\times 1$ matrices, i.e. scalars, where we can determine the determinant using 1. The reason why there is the index $i$ in 2. is the following relationship:

Theorem: Laplace Expansion.
For any $i^*, j^*\in\{1,\ldots,n\}$ , it holds that

$\det(A) = \sum_{j=1}^n (-1)^{i^*+j}a_{i^*j}\det(A_{-i^*j}) = \sum_{i=1}^n (-1)^{i+j^*}a_{ij^*}\det(A_{-ij^*}).$

Typically, we would write down the definition without the use of the star, but I put it there to emphasize that the respective index is fixed. If we fix a row index $i$ to calculate $\det(A)$ , we call the computation method a Laplace expansion by the $i$ -th row, if we fix the column index $j$ , we call it a column expansion by the $j$ -th column. This method is the general way how we compute determinants. However, it is quite computationally extensive, and luckily, most matrices that we deal with analytically (rather than with a computer who doesn’t mind lengthy calculations) are of manageable size where we have formulas for the determinant.

Proposition: Determinants of “small” Matrices.

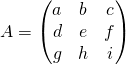If $n=2$ and $A = \begin{pmatrix} a & b\\c&d\end{pmatrix}$ , then $\det(A) = ad - bc$ .
If $n=3$ and $A = \begin{pmatrix} a & b &c\\d&e&f\\g&h&i\end{pmatrix}$ , then $\det(A) = aei + bfg + cdh - (ceg + bdi + afh)$ .

For 1., we can understand the rule using e.g. the Laplace expansion by the first row: note that $A_{-11} = (d), A_{-12} = (c), A_{-21} = (b)$ and $A_{-22} = (a)$ . Thus, we have

$\begin{split}\det(A) &= \sum_{j=1}^2 (-1)^{1+j}a_{1j}\det(A_{-1j}) = (-1)^{2}a_{11}\det(A_{-11}) + (-1)^{3}a_{12}\det(A_{-12}) \\&= 1\cdot a\cdot \det(d) + (-1)\cdot b\cdot \det(c) = ad-bc. \end{split}$

As an exercise and to convince you of the Laplace expansion, try expanding by the second column and verify that you get the same formula. You can also try to verify point 2. of this proposition using the Laplace expansion method if you desire some practice.

Graphically, we can think about the 3×3-determinant as adding the right-diagonal products and subtracting the left-diagonal products:

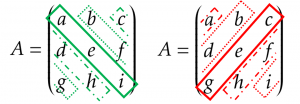
These two results are typically enough for most of our applications, and if not, they at least allow us to break the determinant down to $3\times 3$ rather than $1\times 1$ matrices using the Laplace expansion method, for which we can directly compute the determinants.

Equipped with these rules, two comments on the Laplace method deem worthwhile. First, when we have a row or column containing only one non-zero entry, we can reduce the dimension of determinant computation avoiding a sum: consider the lower-triangular matrix

$A = \begin{pmatrix} 5&2&3&4\\ 0&1&1&0\\ 0&0&-4&3\\ 0&0&0&2\end{pmatrix}.$

The Laplace-expansion for the first column is $\det(A) = \sum_{i=1}^4 (-1)^{i+1}a_{i1}\det(A_{-i1})$ . However, for any $i\neq 1$ , $a_{i1}=0$ , so that the expression reduces to $\det(A) = (-1)^2a_{11}\det(A_{-11}) = 5\det(A_{-11})$ . Applying the $3\times 3$ -rule, it results that $\det(A) = 5\cdot (-8) = -40$ . Second, for triangular matrices generally, the determinant is given by the trace.

Definition: Trace of a Square Matrix.
For a matrix $A\in\mathbb R^{n\times n}$ , the trace $\text{tr}(A)$ is given by the product of diagonal elements, i.e. $\text{tr}(A) = \Pi_{i=1}^n a_{ii}$ .

Proposition: Determinant of a Triangular Matrix.
The determinant of an upper or upper triangular matrix $A\in\mathbb R^{n\times n}$ is given by its trace, i.e. $\det(A) = \text{tr}(A)$ .

The proposition follows from simply iterating on what we have done in the example above for a general matrix: consider the upper triangular matrix

$A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ 0&a_{22}&\cdots & a_{2n}\\ \vdots & \ddots &\ddots &\vdots\\ 0&\cdots&0&a_{nn}\end{pmatrix}.$

Expanding iteratively by the first column, it follows that

$\begin{split}\det(A) &= a_{11} \det \begin{pmatrix} a_{22} & a_{23} & \cdots & a_{2n}\\ 0&a_{32}&\cdots & a_{3n}\\ \vdots & \ddots &\ddots &\vdots\\ 0&\cdots&0&a_{nn}\end{pmatrix} = a_{11} a_{22} \det \begin{pmatrix} a_{33} & a_{34} & \cdots & a_{3n}\\ 0&a_{43}&\cdots & a_{4n}\\ \vdots & \ddots &\ddots &\vdots\\ 0&\cdots&0&a_{nn}\end{pmatrix} \\&= \ldots = \Pi_{i=1}^na_{ii} = \text{tr}(A).\end{split}$

For the lower-triangular matrix, the procedure would be analogous, here, we just have to expand for the first row instead of column iteratively.

The two key take-aways are that when you have to compute the determinant of big matrices by hand, look for rows and/or columns with many zeros to apply the Laplace-expansion, or if you’re lucky and face a lower or upper triangular matrix, you can directly compute the determinant from the diagonal (this is of course especially true for diagonal matrices, since they are both upper and upper triangular!). The latter fact is nice especially because the elementary matrix operations introduced above affect the determinant in a tractable way, so that it is possible to avoid Laplace altogether:

Theorem: Determinant and Elementary Operations.
Let $A\in\mathbb R^{n\times n}$ and $\tilde A$ the resulting matrix for the respective elementary operation. Then,

1. for operation (E1) (interchange of two rows), we have $\det(\tilde A) = -\det (A)$ , i.e. the interchange of rows changes the sign of the determinant,
2. for operation (E2) (row multiplication with a scalar $\lambda\neq 0$ ), $\det(\tilde A) = \lambda\det(A)$ ,
3. for operation (E3) (addition of multiple of row to another row), $\det(\tilde A) = \det(A)$ , i.e. (E3) does not change the determinant.

Another important fact that will be helpful frequently is the following:

Theorem: Determinant of the Product.
Let $A,B\in\mathbb R^{n\times n}$ . Then, $\det(AB) = \det(A)\det(B)$ .

Note that in contrast to the product, for the sum, it does not hold in general that $\det(A+B) = \det(A)+\det(B)$ .

Now that we now how to compute a determinant, we care about its role in existence and determination of inverse matrices. As already stated above, the rule we will rely on is inherently simple:

Theorem: Determinant and Invertibility.
Let $A\in\mathbb R^{n\times n}$ . Then, $A$ is invertible if and only if $\det(A) \neq 0$ .

The “only if” part is rather simple: suppose that $A$ is invertible. Note that $\det(\mathbf{I_n}) = 1$ (cf. Proposition “Determinant of a Triangular Matrix”). Then,

$1 = \det(\mathbf{I_n}) = \det(AA^{-1}) = \det(A)\det(A^{-1}).$

Therefore, $\det(A)\neq 0$ . Moreover, this equation immediately establishes the following corollary:

Corollary: Determinant of the Inverse Matrix.
Let $A\in\mathbb R^{n\times n}$ and suppose that $A$ is invertible. Then, $\det(A^{-1}) = 1/\det(A)$ .

The key take-away here is that invertibility is equivalent to a non-zero determinant. Consequently, because invertibility implies unique existence of the solution, so does a non-zero determinant. While the general determinant concept is a little notation-intensive, computation is easy for smaller matrices. Thus, the determinant criterion represents the most common invertibility check for “small” matrices or respectively, the most common unique solution check for “small” systems of linear equations when we have as many unknowns as equations.

As the take-away on how to compute determinants, we can summarize the following:

- Small matrix? Apply the rules for 2×2 or 3×3 matrices.
- Triangular or diagonal matrix? Use the trace!
- Otherwise: perform a Laplace expansion for a convenient row/column – look for zeros!

Rank of a Matrix

Clearly, we don’t always find ourselves in the comfortable situation that we have as many equations as unknowns. To determine whether these systems have a unique solution, we need to understand the rank of a matrix. The rank of a matrix links closely to our discussion of linear dependence in Chapter 1.

To limit the formal complexity of the discussion, in contrast to the companion script, we still focus on square systems here. This will allow us to talk about the role the rank of a matrix plays for it’s invertibility. In an excursion into non-square systems at the end of this section, yyou will learn what the discussion below implies for solving non-square systems.

Let’s again consider the equation system in matrix notation, $Ax=b$ , and assume that $A$ is square. When writing $A$ in column notation as $A = (a_1,a_2,\ldots,a_n)$ , $a_i\in\mathbb R^n$ for all $i$ , it is straightforward to check that $Ax = \sum_{i=1}^n x_ia_i$ (try to verify it for the $3\times 3$ case).

Thus, the LHS of the system is nothing but a linear combination of the columns of $A$ with coefficients $x=(x_1,\ldots,x_n)'$ ! Therefore, the problem of solving the system of linear equations can be rephrased as as looking for the linear combination coefficients for the columns of our coefficient matrix $A$ that yields the vector $b$ ! Let us illustrate this abstract characterization with an example.

Consider the following system:

$\begin{split} x_1 + 2x_2 &= 2\\ x_1-x_2 &= 0 \end{split}$

with associated matrix form

$Ax = \begin{pmatrix} 1 & 2\\ 1 & -1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}= \begin{pmatrix} 2 \\ 0 \end{pmatrix} = b \hspace{0.5cm}\Leftrightarrow\hspace{0.5cm} \begin{pmatrix} 2 \\ 0 \end{pmatrix} = \begin{pmatrix} 1\cdot x_1 + 2\cdot x_2\\ 1\cdot x_1 + (-1)\cdot x_2 \end{pmatrix} = x_1 \begin{pmatrix} 1 \\ 1 \end{pmatrix} + x_2 \begin{pmatrix} 2 \\ -1 \end{pmatrix}.$

Recall that the linear combination coefficients can be viewed as combination magnitudes (or weights) of the vectors $a_1,\ldots,a_n$ . Thus, less formally, we are looking for the distance we need to go in every direction indicated by a column of $A$ to arrive at the point $b$ . Geometrically, you can imagine the problem like this:

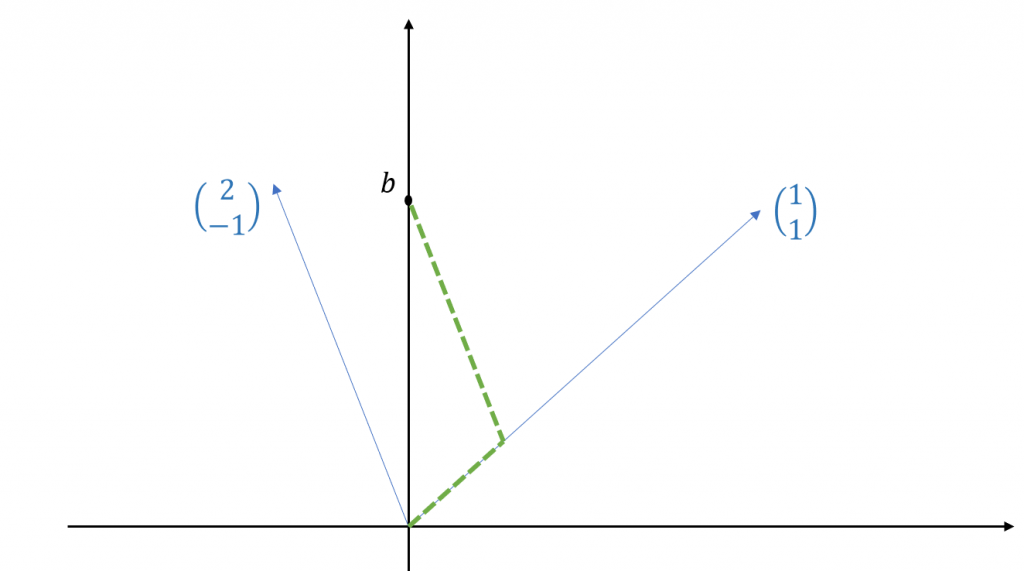
Feel encouraged to repeat this graphical exercise for other points $b\in\mathbb R^2$ ; you should always arrive at a unique solution for the linear combination coefficients. The fundamental reason is that the columns of $A$ , $(1,1)'$ and $(2,-1)'$ are linearly independent. Think a second about what it would mean geometrically if they were linearly dependent before continuing.

Done? Good! In case of linear dependence, the points lie on the same line through the origin, and either, $b$ does not lie on this line and we never arrive there, i.e. there are no solutions, or it does, and an infinite number of combinations of the vectors can be used to arrive at $b$ . Either way, there is no unique solution to the system.

Now, it is time to formalize the idea of the “number of directions” that are reached by a matrix and whether “a point $b$ can be reached combining the columns of $A$ “.

Definition: Column Space of a Matrix.
Let $A\in\mathbb R^{m\times n}$ with columns $a_1,\ldots,a_n\in\mathbb R^m$ , i.e. $A=(a_1,\ldots,a_n)$ . Then, the column space Co $(A)$ of $A$ is the space “spanned by” these columns, i.e.

$Co(A) = \{x\in\mathbb R^m: (\exists \lambda_1,\ldots,\lambda_m: x = \sum_{j=1}^m \lambda_j a_j)\}.$

Analogously, we define the row space as the space spanned by the rows of $A$ . As a technical detail, note that we called the column space a “space”, and recall from chapter 1 that formally, this means that we need to think about the basis operations that we use. Here, we assume that as a space of real-valued vectors, we use the same operations as for the $\mathbb R^n$ .

Definition: Rank of a Matrix.
Let $A\in\mathbb R^{n\times m}$ . Then, the column (row) rank of $A$ is the dimension of the column (row) space of $A$ . It coincides with the number of linearly independent columns (rows) of $A$ and is denoted as rk $(A)$ , rank $(A)$ or rk $A$ .

You may wonder why we use the same notation for the column and row rank, respectively. This is due to the following fact:

Theorem: Column Rank = Row Rank.
Let $A\in\mathbb R^{n\times m}$ . Then, the column rank and the row rank of $A$ coincide.

Thus, “the rank” of $A$ , rk $(A)$ is a well-defined object, and it does not matter whether we compute it from the columns or rows.

Definition: Full Rank.
Consider a matrix $A\in\mathbb R^{n\times m}$ . Then, $A$ has full row rank if rk $(A)=n$ and $A$ has full column rank if rk $(A) = m$ . If the matrix is square, $A$ has full rank if rk $(A) = n = m$ .

Since column and row rank and at most $n$ rows and $m$ columns can be linearly independent, we get the following result:

Corollary: A Bound for the Rank.
Let $A\in\mathbb R^{n\times m}$ . Then, rk $(A)\leq \min\{n,m\}$ .

From the definitions above, you should be able to observe that the rank captures the number of directions into which we can move using the columns of $A$ , and that the column space is the set of all points we can reach using linear combinations of $A$ ‘s columns. Consequently, a solution exists if and only if $b\in Co(A)$ , and it is unique, i.e. there is at most one way to “reach” it, if and only if $A$ does not have more columns than $rk(A)$ , that is, if every column captures an independent direction not reached by the remaining columns. In the case of a square $n\times n$ system, this reduces to $rk(A)=n$ .

Let us rephrase this: if (and only if) $rk(A)=n$ , then (i) every column captures an independent direction which ensures that there is no multitude of solutions, and (ii) the matrix $A$ reaches $n$ different directions, that is, it allows extension alongside every direction in the $\mathbb R^n$ , so that every point $b\in\mathbb R^n$ can be reached: $Co(A) = \mathbb R^n$ ! To summarize:

Theorem: Rank Condition for Square Systems.
Let $A\in\mathbb R^{n\times n}$ and $b\in\mathbb R^n$ . Then, $A$ is invertible or respectively, the system $Ax=b$ has a unique solution if and only if $A$ has full rank, i.e. $rk(A)=n$ .

Above, we had seen that inverting a matrix can be done by bringing it to identity form using elementary operations. Note that this means that any intermediate matrix that we get in the process of applying the elementary operations is invertible as well, since it can also be brought to identity form using only elementary operations. This means that for an invertible matrix $A$ with full rank $rk(A)=n$ , all intermediate matrices of the inversion procedure must also have full rank! This is indeed true:

Theorem: Rank and Elementary Operations.
Let $A\in\mathbb R^{n\times m}$ . Then, rk $(A)$ is invariant to elementary operations, i.e. for any $\tilde A$ associated with operations (E1) to (E3), rk $(\tilde A) =$ rk $(A)$ .

To test your understanding, think about the following question: Consider an upper triangular matrix

$A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ 0 & a_{22} & \ddots & \vdots \\ \vdots & \ddots & \ddots & a_{n-1,n} \\ 0 & \cdots & 0 & a_{nn} \end{pmatrix}.$

When are the columns of $A$ linearly independent (think of the linear independence test, and go over the rows backwards)? What does this mean for the determinant?

The columns of $A$ are linearly independent if and only if the diagonal entries are all non-zero, i.e. $\forall i\in\{1,\ldots,n\}: a_{ii} = 0$ . This is precisely the condition for a non-zero determinant. This implies that the non-zero determinant and the full rank of the upper triangular matrix are equivalent. Indeed, this holds for any initial, square matrix $A$ that we could start from. To see this directly, note that the non-zero determinant and the full rank are both equivalent to invertability of the matrix, and therefore also equivalent to each other.

Excursion: Non-square Systems

As already stated above, this course restricts attention to square systems. Of course, in applications, nothing guarantees that we will always work with such systems. This excursion is concerned with the intuition of non-square systems, without going into any formal, mathematical details.

Above, we had just seen that unique solutions exist in “square systems” with an invertible (square) matrix $A$ . Indeed, it turns out that more generally, unless the system can be “reduced” to a square system with invertible matrix $A$ , there can be no unique solution! This follows from isolated consideration of the multiple cases of general equation systems. Here, it is helpful to think of the number of rows of the matrix $A\in\mathbb R^{n\times m}$ in $Ax = b$ as the “information content” of the equation system, that is, the number of pieces of information that we have for the vector $x\in\mathbb R^m$ .

First, if we have less equations than unknowns (an “under-identified” system, $n<m$ ), there are always more columns than dimensions, so that it remains ambiguous which columns to combine to arrive at $b$ . We can think about this as that the system can never have enough information to uniquely pin down the solution, as we would require at least $m$ restrictions on the value $x\in\mathbb R^m$ should take, one for every entry, but we only have $n<m$ . Still, if multiple columns are linearly dependent, it can be the case that $Co(A)\neq \mathbb R^n$ , and certain vectors $b\in\mathbb R^n$ may not be reached using the columns of $A$ , such that there might be no solution at all.

Conversely, with more equations than unknowns (an “over-identified” system, $n>m$ ), it can never be that $Co(A) = \mathbb R^n$ as the $m$ columns of $A$ can reach at most $m<n$ independent directions of the $\mathbb R^n$ . This means that some rows contain either contradictory or redundant information given the statements in the other rows. Roughly, the $i$ -th row $a'_i$ of $A$ is contradictory if the corresponding entry in $b$ , $b_i$ , can not be reached through choosing $x$ in a way consistent with the other rows, and it is redundant if $a'_i x = b$ is already implied by the restrictions imposed through the other rows (i.e., the other equations). Redundant information can be left out of the system without changing the result, but reducing the row dimension by 1. To see conflicting and redundant information in very simplistic examples, consider the following two equation systems:

$\begin{matrix} 4 x_1 & + & 2 x_2 &=& 6\\ x_1 & - & x_2 &=& 0\\ x_1 & + & x_2 &=& 4 \end{matrix} \hspace{0.5cm}\text{and}\hspace{0.5cm} \begin{matrix} 4 x_1 & + & 2 x_2 &=& 6\\ x_1 & - & x_2 &=& 0\\ x_1 & + & x_2 &=& 2 \end{matrix}$

In both systems, we know per the second equation that $x_1 = x_2$ . In the first, we get $6x_1 = 6$ and $2x_1 = 4$ from the first and third equations, respectively, an information conflict. In the second, equations 1 and 3 give $6x_1 = 6$ and $2x_1 = 2$ , one of which is redundant because the other is already sufficient to conclude that $x_1 = 1$ .

A unique solution may potentially be obtained if (i) there is no conflicting information and (ii) we can eliminate enough redundant information to arrive at an equivalent square system. For this system, we can perform our usual determinant check.

Eigenvalues, Eigenvectors and Definiteness of a Matrix

The concepts of eigenvalues and -vectors and matrix definiteness have a purpose far beyond the context of invertibility, and presumably, you will come across them frequently throughout your master studies. However, as they don’t really belong to any of the overarching topics discussed in this course, and since they are also quite handy to check for invertability in square systems, their introduction is placed here. Before getting started, as with the determinant, make sure to keep in mind that only square matrices have eigenvalues and definiteness! Thus, unlike the rank, the associated invertibility criteria do not generalize to non-square systems!

Definition: Eigenvectors and -values.
Consider a square matrix $A\in\mathbb R^{n \times n}$ . Then, $x \in \mathbb{R}^n\backslash\{\mathbf 0\}$ is said to be an eigenvector of $A$ if there exists a $\lambda\in\mathbb{R}$ such that $A x=\lambda x$ . $\lambda$ is then called an eigenvalue of $A$ .

To practice again some quantifier notation, you can try to write down the definition of an eigenvalue: We call $\lambda\in\mathbb R$ an eigenvalue of $A$ if

$\exists x\in\mathbb R^n\backslash\{\mathbf 0\}:(Ax=\lambda x)$ .

Let’s think about intuitively what it means if $Ax = \lambda x$ : clearly, $Ax$ and $x$ are linearly dependent: $\lambda x + (-1)Ax = 0$ , and thus, $x$ and $Ax$ lie on the same line through the origin! Note that if $x=\mathbf 0$ , then trivially, for any $\lambda\in\mathbb R$ it holds that $\lambda x = Ax = \mathbf 0$ , so that any $\lambda\in\mathbb R$ would constitute an eigenvalue and make the definition meaningless. This is why we require that $x\neq\mathbf 0$ . On the other hand, $0$ can indeed be an eigenvalue, namely if there exists $x\neq \mathbf 0$ so that $Ax = \mathbf 0$ . Then, geometrically, $Ax$ is indeed equal to the origin.

The following focuses on the answers to two questions: (i) how can we find eigenvalues (and associated eigenvectors)? and (ii) what do the eigenvalues tell us about invertibility of the matrix?

Starting with (i), we can re-write the search for an eigenvector $x$ of $A$ for an eigenvalue candidate $\lambda\in\mathbb R$ as a special system of linear equations: If $x$ is an eigenvector of $A$ for $\lambda$ ,

$Ax = \lambda x = \lambda \cdot (\mathbf{I_n}x)\hspace{0.5cm}\Leftrightarrow\hspace{0.5cm} \mathbf 0 = Ax - \lambda\mathbf{I_n}x = (A - \lambda\mathbf{I_n})x.$

Thus, we have a square system of equations $C_\lambda x = b$ with coefficient matrix $C_\lambda = A - \lambda\mathbf{I_n}$ and solution vector $b=\mathbf 0$ . Now, how does this help? Note that if there is an eigenvector $x$ of $\lambda$ , it is not unique: if $Ax=\lambda x$ , for any $c\neq 0$ , $A(cx) = \lambda (cx)$ , and $\tilde x = cx$ is also an eigenvector of $A$ associated with $\lambda$ ! Thus, we are looking precisely for the situation where the square system does not have a unique solution, i.e. where $\det(C_\lambda) = 0$ and $C_{\lambda}$ is not invertible! This suggests that we can find the eigenvalues of $A$ by solving

$P(\lambda) = \det(A-\lambda \mathbf{I_n}) = 0,$

i.e. by setting the characteristic polynomial of $A$ to zero, or respectively, by finding its roots. You may already have seen applications of this method in different contexts.

Let us consider an example here to facilitate understanding. Let $A = \begin{pmatrix} 3 & 2\\ 1 & 2\end{pmatrix}$ . Then,

$\begin{split} P(\lambda) & = \det(A-\lambda I) = \det\left (\begin{pmatrix} 3 & 2\\ 1 & 2\end{pmatrix} - \begin{pmatrix} \lambda & 0\\ 0 & \lambda\end{pmatrix}\right ) = \det\begin{pmatrix} 3-\lambda & 2\\ 1 & 2-\lambda\end{pmatrix}\\ &= (3-\lambda)(2-\lambda) - 2\cdot 1 = 6 - 2\lambda - 3\lambda + \lambda^2 - 2 = \lambda^2 - 5\lambda + 4. \end{split}$

Solving $P(\lambda)=0$ can be done with the p-q-formula: $P(\lambda)=0$ is equivalent to

$\lambda\in\left \{-\frac{-5}{2}\pm \sqrt{\left (\frac{-5}{2}\right )^2 - 4}\right \} = \left \{\frac{5}{2}\pm \sqrt{\frac{25-16}{4}}\right \} = \left \{\frac{5}{2}\pm \frac{3}{2}\right \} = \{1,4\}.$

Consequently, our eigenvalue candidates are $\lambda_1=1$ and $\lambda_2 = 4$ . To find the eigenvectors, we have to solve the equation system: for $\lambda_1=1$ , $C_1 = A-1\cdot\mathbf{I_n} = \begin{pmatrix} 3-1 & 2\\ 1 & 2-1\end{pmatrix} = \begin{pmatrix} 2 & 2\\ 1 & 1\end{pmatrix}$ . Clearly, you can see that this matrix does not have full rank and thus a multitude of solutions. $C_1x = \mathbf 0$ is equivalent to $x_1+x_2 = 0$ or respectively, $x_1 = -x_2$ . Thus, the eigenvectors of $\lambda_1 = 1$ are multiples of $(1,-1)'$ . The set of all these vectors is $\left \{c\cdot\begin{pmatrix}1\\-1\end{pmatrix}:c\in\mathbb R\right \}$ is the so-called eigenspace of $\lambda_1=1$ . For $\lambda=4, C_4 = A-4\cdot\mathbf{I_n} = \begin{pmatrix} 3-4 & 2\\ 1 & 2-4\end{pmatrix} = \begin{pmatrix} -1 & 2\\ 1 & -2\end{pmatrix}$ , the eigenvectors are multiples of $(2,1)'$ and the eigenspace of $\lambda_1=4$ is $\left \{c\cdot\begin{pmatrix}2\\1\end{pmatrix}:c\in\mathbb R\right \}$ . Note that an eigenvalue may occur “more than once” and generally be associated with multiple linearly independent eigenvectors. In such a case, we still define the eigenspace as the set of linear combinations of all linearly independent eigenvectors associated with the eigenvalue.

To the second question, how do eigenvalues help in determining invertibility? This is very simple:

Proposition: Eigenvalues and Invertibility.
Let $A\in\mathbb R^{n\times n}$ . Then, $A$ is invertible if and only if all eigenvalues of $A$ are non-zero.

The simple reason for this relationship is that $A$ is invertible if and only if

$0\neq \det(A) = \det(A-0\cdot\mathbf{I_n}),$

which is the case if and only if $0$ is not an eigenvalue of $A$ .

The practical value is that sometimes, you may have already computed the eigenvalues of a matrix before investigating its invertibility. Then, this proposition can help you avoid the additional step of computing the determinant.

Now, coming to the last concept: definiteness. Let’s first look at the definition:

Definition: Definiteness of a Matrix.
A symmetric square matrix $A\in\mathbb R^{n\times n}$ is called

- positive semi-definite if $\forall x\in\mathbb R^n: x'Ax\geq 0$
- negative semi-definite if $\forall x\in\mathbb R^n: x'Ax\leq 0$
- positive definite if $\forall x\in\mathbb R^n\backslash\{\mathbf 0\}: x'Ax > 0$
- negative definite if $\forall x\in\mathbb R^n\backslash\{\mathbf 0\}: x'Ax < 0$

Otherwise, it is called indefinite.

Note that the concept not only applies only to square matrices, but also requires them to be symmetric! Further, we exclude the zero vector from definiteness because $\mathbf 0' A\mathbf 0 = 0$ for all matrices $A$ . The concept’s relation to invertibility is the given through the following characterization:

Proposition: Definiteness and Eigenvalues.
A symmetric square matrix $A\in\mathbb R^{n\times n}$ is

positive (negative) definite if and only if all eigenvalues of $A$ are strictly positive (negative).
positive (negative) semi-definite if and only if all eigenvalues of $A$ are strictly non-negative (non-positive).

To see this relationship intuitively, note that for any eigenvalue $\lambda$ with eigenvector $x_\lambda\in\mathbb R^n\backslash\{\mathbf 0\}$ , it holds that

$x_\lambda'Ax_\lambda = x_\lambda' (\lambda x_\lambda) = \lambda \|x_\lambda\|_2^2$

where $\|\cdot\|_2$ is the Euclidean norm (recall the sum-of-squares property of the scalar product of a vector with itself). Since the norm is non-negative, the sign of $x_\lambda'Ax_\lambda$ corresponds to the sign of $\lambda$ .

Thus, with the two previous Propositions, the following corollary emerges:

Corollary: Definiteness and Invertibility.
If $A\in\mathbb R^{n\times n}$ is symmetric and positive definite or negative definite, it is invertible.

This follows because positive and negative definiteness rule out zero eigenvalues. Thus, positive and negative definiteness are sufficient conditions for invertibility!

Excursion: An Example of Positive Definiteness

Definiteness is a useful criterion especially for matrices of the form $A = X'X$ with a general matrix $X$ of dimension $n\times k$ . The form $X'X$ ensures that the matrix $A$ is both square and symmetric, and hence, its definiteness is defined. Further, it is at least positive semi-definite, as for any $v\in\mathbb R^{k}$ ,

$v'X'Xv = (Xv)'Xv = \|Xv\|_2^2\geq 0.$

To achieve positive definiteness, it must be ruled out that $Xv = \mathbf 0$ , as otherwise, the sum of squares is always strictly positive. Suppose that $v\neq \mathbf 0$ . Then, what does $Xv=0$ mean? We can re-write $X = (x_1,\ldots,x_{k})$ in column notation. Then, it is easily verified that $Xv = v_1 x_1 + \ldots + v_{k} x_{k}$ . Thus, if $Xv = \mathbf 0$ for $v\neq\mathbf 0$ , there exists a linear combination of the columns of $X$ with non-zero coefficients that is equal to zero. Thus, some columns of $X$ must be linearly dependent, i.e. $rk(X)<k$ .

Therefore, any matrix $A=X'X$ where $X$ has full column rank is invertible by the definiteness criterion. This comes in handy for instance in the context of the OLS-estimator that we had already briefly considered above, $\hat\beta^{OLS}:= (X'X)^{-1}X'y$ . Indeed, in the OLS context, we make a specific “no-multi-collinearity” assumption that ensures $rk(X)=k$ .

Computing Inverse Matrices: the Gauß-Jordan Algorithm

After the extensive discussion of invertibility above, let’s finally discuss how, if we have established invertibility, we can actually compute the inverse matrix. Indeed, if you managed to follow what we did thus far, you actually know already how this works: we can apply the same elementary operations that we use to transform an invertible matrix $A$ to the identity matrix to an identity matrix and arrive at the inverse.

Before turning to an example on how this works, we need to briefly worry about whether this always works! Thus far, we only know that when we can apply the suggested procedure, then we have found the inverse, but it remains to establish formally that it also holds that whenever there exists an inverse, the suggested procedure will identify it. This is indeed true:

Theorem: Gauß-Jordan Algorithm Validity.
Suppose that $A\in\mathbb R^{n\times n}$ is an invertible matrix. Then, we can apply elementary operations $E_1,\ldots, E_k$ in ascending order of the index to $A$ to arrive at the identity matrix $\mathbf{I_n}$ , and the inverse can be determined as $A^{-1} = E_k\cdot\ldots\cdot E_1$ .

The interested reader can find the proof in the companion script to develop a deeper understanding of why this relationship holds.

In applying the procedure in practice, to keep things tractable, we write the identity matrix next to the matrix to be inverted and perform operations iteratively. To convert $A$ to the identity, you will first want to bring it to upper triangular form; as we have seen, from there on out, it’s really simple.

Let us consider an example: Start from the matrix

$A = \begin{pmatrix} 2 & -1 & 0\\ -1 & 2 & -1\\ 0 & -1 & 2\end{pmatrix}.$

First, we want to know whether it is invertible — a quick check of the determinant criterion (that we can apply because the matrix is square), using e.g. our $3\times 3$ formula (do it!), yields $\det(A) = 4 \neq 0$ , so the matrix is indeed invertible. So, let’s start the procedure by writing the matrix next to an identity matrix of appropriate dimension:

$\begin{pmatrix} 2 & -1 & 0\\ -1 & 2 & -1\\ 0 & -1 & 2 \end{pmatrix} \hspace{0.5cm} \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}$

Our first goal is to get a $2\times 2$ triangular block in the upper left corner — this is always a good start. For this, because the (1,1) entry is non-zero, we add $1/2$ times row 1 to row 2 to eliminate the $-1$ at position (2,1) (if the (1,1) entry was zero, we could simply exchange rows). Applying this transformation to both matrices gives

$\begin{pmatrix} 2 & -1 & 0\\ 0 & 3/2 & -1\\ 0 & -1 & 2 \end{pmatrix} \hspace{0.5cm} \begin{pmatrix} 1 & 0 & 0\\ 1/2 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}$

Now, note that we want ones on the diagonal. Thus, we multiply rows 1 and 2 by $1/2$ and $2/3$ , respectively:

$\begin{pmatrix} 1 & -1/2 & 0\\ 0 & 1 & -2/3\\ 0 & -1 & 2 \end{pmatrix} \hspace{0.5cm} \begin{pmatrix} 1/2 & 0 & 0\\ 1/3 & 2/3 & 0\\ 0 & 0 & 1 \end{pmatrix}$

One more step to get to upper triangular form — add row 2 to row 3:

$\begin{pmatrix} 1 & -1/2 & 0\\ 0 & 1 & -2/3\\ 0 & 0 & 4/3 \end{pmatrix} \hspace{0.5cm} \begin{pmatrix} 1/2 & 0 & 0\\ 1/3 & 2/3 & 0\\ 1/3 & 2/3 & 1 \end{pmatrix}$

Let’s get our last one on the diagonal by multiplying the last column with $3/4$ :

$\begin{pmatrix} 1 & -1/2 & 0\\ 0 & 1 & -2/3\\ 0 & 0 & 1 \end{pmatrix} \hspace{0.5cm} \begin{pmatrix} 1/2 & 0 & 0\\ 1/3 & 2/3 & 0\\ 1/4 & 1/2 & 3/4 \end{pmatrix}$

Now, we have our triangular form and we’re almost there. First, get rid of the non-zero entry in position (2,3) by adding $2/3$ times row 3 to row 2:

$\begin{pmatrix} 1 & -1/2 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} \hspace{0.5cm} \begin{pmatrix} 1/2 & 0 & 0\\ 1/2 & 1 & 1/2\\ 1/4 & 1/2 & 3/4 \end{pmatrix}$

Finally, it remains to add $1/2$ times row 2 to row $1$ :

$\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} \hspace{0.5cm} \begin{pmatrix} 3/4 & 1/2 & 1/4\\ 1/2 & 1 & 1/2\\ 1/4 & 1/2 & 3/4 \end{pmatrix}$

Thus, our algorithm tells us that 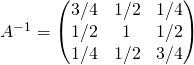$A^{-1} = \begin{pmatrix} 3/4 & 1/2 & 1/4\\ 1/2 & 1 & 1/2\\ 1/4 & 1/2 & 3/4 \end{pmatrix}$ . If you’re suspicious and don’t fully trust the abstract concept, verify that $A A^{-1} = \mathbf{I_n}$ !

The example given here was very extensive, usually, to save space and time, you would produce the zeros for the triangular form in the same step where you set the diagonal elements to one. If doing so, you may only need three steps, or even less, depending on how many transformations you manage to track in one step. Being less extensive will help you save time in exams or at problem sets, but when going fast you are also more prone to errors, so watch out!

Finally, when considering a $2\times 2$ matrix, there is a rule that allows us to avoid the algorithm:

Proposition: Inverse of a $2\times 2$ Matrix.
Consider the matrix $A = \begin{pmatrix} a & b \\ c & d\end{pmatrix}$ where $ad\neq bc$ . Then,

$A^{-1} = \frac{1}{\det(A)} \begin{pmatrix} d & -b \\ -c & a\end{pmatrix} = \frac{1}{ad-bc} \begin{pmatrix} d & -b \\ -c & a\end{pmatrix}.$

This fact gives the arguably quickest way to compute the inverse for any $2\times 2$ matrix and it is worthwhile memorizing.

Wrap-Up

Let us summarize what we have concluded for equation systems and invertibility:

- A square system of equations $Ax=b$ has a unique solutions if and only if the matrix $A$ is invertible. Then, the solution $x^*$ satisfies $x^* = A^{-1}b$ .
- A square matrix is invertible if and only if either of the following equivalent conditions hold:
  1. $\det(A) \neq 0$ ,
  2. rk $(A) = n$ ,
  3. When transforming $A$ to triangular form $\tilde A$ , the diagonal of $\tilde A$ has only non-zero entries,
  4. All eigenvalues of $A$ are non-zero.
- Further, if $A$ is symmetric, sufficient invertibility conditions are positive and negative definiteness.
- We can invert a matrix using the Gauß-Jordan algorithm or a rule if the matrix is $2\times 2$ .

Before moving on, if you feel like testing your understanding of the concepts discussed since the last quiz, you can take a short quiz found here.