An overview of this chapter’s contents and take-aways can be found here.
We have seen a lot of new concepts in the last three chapters. This chapter is concerned with putting all the pieces together and uses them to give you an in-depth understanding of the economist’s favorite exercise: optimization. As anyone with some background in economics should know by now, optimization is virtually everywhere in economic considerations: households optimize the allocation of their time budget to working for income and leisure, optimally divide their budget into consumption and savings over time, optimize the composition of their consumption bundles, firms optimize input use, output quantities, factor composition (i.e., the production shares of labor and capital, respectively), and governments (or: social planners) seek to maximize welfare through public goods provision, minimize negative externalities through market regulations, and optimize the social value generated from each unit of tax money over a broad portfolio of possible actions. In doing so, the agents we consider are almost always constrained in some form: households do not have infinitely much time, firms face output targets, and governments can not spend more money as is generated from tax revenue. Thus, to be able to track all these issues mathematically, we as economists need to firmly understand the techniques of constrained optimization.
Table of Contents
As a first step to solving it, let us consider how to write down an optimization problem mathematically.
![Rendered by QuickLaTeX.com \[ (\mathcal{P}_{min}) \hspace{2cm} \begin{aligned} & \underset{x\in \text{ dom}(f)}{\text{minimize}} & & f(x)\\ & \text{subject to} & & g_i(x) = 0, \; i = 1, \ldots, m.\\ & & & h_i(x) \leq 0, \; i = 1, \ldots, k.\\ \end{aligned} \]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-6e638c936d460e92e3b704316496d856_l3.png)
![Rendered by QuickLaTeX.com \[ (\mathcal{P}_{max}) \hspace{2cm} \begin{aligned} & \underset{x\in \text{ dom}(f)}{\text{maximize}} & & f(x)\\ & \text{subject to} & & g_i(x) = 0, \; i = 1, \ldots, m.\\ & & & h_i(x) \leq 0, \; i = 1, \ldots, k.\\ \end{aligned} \]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-676f1ad09bc4a6bd006478c31883e4c3_l3.png)
Here, ![]() ,
, ![]() and
and ![]() ,
, ![]() are functions mapping from the set of
are functions mapping from the set of ![]() ‘s, the domain dom
‘s, the domain dom![]() , to
, to ![]() (i.e., there is only one quantity to be maximized, not a vector). We call
(i.e., there is only one quantity to be maximized, not a vector). We call ![]() our objective function and
our objective function and ![]() the choice variables. In words, we are looking for the
the choice variables. In words, we are looking for the ![]() in the domain of
in the domain of ![]() that yields either the smallest (or largest) value
that yields either the smallest (or largest) value ![]() can possibly attain when we require that the functions
can possibly attain when we require that the functions ![]() must attain the value
must attain the value ![]() and
and ![]() can not lie strictly above
can not lie strictly above ![]() — we want to minimize (or maximize)
— we want to minimize (or maximize) ![]() subject to the equality constraints given by the
subject to the equality constraints given by the ![]() and the inequality constraints by
and the inequality constraints by ![]() . You may wonder if it is not a restrictive formulation to have only equality constraints requiring a function to be equal to zero, and “less or equal” inequalities. Indeed, it is not: note that we can always re-write a condition
. You may wonder if it is not a restrictive formulation to have only equality constraints requiring a function to be equal to zero, and “less or equal” inequalities. Indeed, it is not: note that we can always re-write a condition ![]() as
as ![]() and
and ![]() as
as ![]() . Lastly, if
. Lastly, if ![]() , we say that the problem is unconstrained.
, we say that the problem is unconstrained.
Throughout the entire chapter, we will most often consider maximization problems, as it is the problem more common in economics. Indeed, every minimization problem with objective ![]() can be equivalently solved as the maximization problem of
can be equivalently solved as the maximization problem of ![]() , such that this approach is without loss of generality. Still, conceptually, maximization and minimization problems are of course distinct (one example is the different second order condition for the solution).
, such that this approach is without loss of generality. Still, conceptually, maximization and minimization problems are of course distinct (one example is the different second order condition for the solution).
Before moving on, a few words on our conceptual approach: as with multivariate differentiation, the elaborations in the online course will focus on more on the “how” of optimization rather than the “why”, which is paid more attention in the companion script and perhaps our course week. Still, we do discuss why the conditions we use in our approaches to solving optimization problems are valid so as to allow you to understand what you are doing when applying them, which should make your applications less error-prone. In doing so, we focus again on intuitive and suggestive reasoning, and omit the formal proofs. While it is of course more important that you know how to correctly apply the methods of constrained optimization and you need not master their formal justification completely just yet, feel encouraged to dig deeper into the formalities behind this issue when you find the time! Due to the importance of constrained optimization in economics, any good economist should be thoroughly aware of why his or her approach to solving these optimization problems works, and once you dig deeper into economic or econometric theory, you will find that formally understanding constrained optimization methods is a necessary condition for being able to deal with the more advanced techniques and more complex issues studied there. So while the details of multivariate differentiation are good to know, the ones of constrained optimization are the ones you are strongly advised to familiarize yourself with at least until the end of your master’s studies – but the sooner the better, since doing so will facilitate any application you see during your coursework and also exams, and also greatly train your skill of dealing with Taylor expansions.
Before digging into the whole process of optimization, it is wise to (i) formally define what we are looking for (i.e. maximum or minimum) and (ii) evaluate how “likely” it is that we will find it by looking at specific properties of the objective function and of its domain.
Definition: Extremum: Minimum and Maximum of a Set.
Let ![]() . Then,
. Then, ![]() is called the maximum of
is called the maximum of ![]() , denoted
, denoted ![]() , if
, if ![]() and
and ![]() . Conversely,
. Conversely, ![]() is called the minimum of
is called the minimum of ![]() , denoted
, denoted ![]() , if
, if ![]() and
and ![]() .
. ![]() is called an extremum of
is called an extremum of ![]() if
if ![]() or
or ![]() .
.
Verbally, ![]() is the maximum of
is the maximum of ![]() if
if ![]() is the smallest number greater or equal than all elements of
is the smallest number greater or equal than all elements of ![]() , and it is also contained in
, and it is also contained in ![]() . More simply put, it is the largest value in the set if there is any such value. This need not be the case, recall that e.g. open intervals
. More simply put, it is the largest value in the set if there is any such value. This need not be the case, recall that e.g. open intervals ![]() neither have a maximum nor a minimum, but only infimum and supremum. However, for sets of real numbers, if there is a minimum or a maximum, it (i) is unique and (ii) coincides with the infimum or the supremum, respectively.
neither have a maximum nor a minimum, but only infimum and supremum. However, for sets of real numbers, if there is a minimum or a maximum, it (i) is unique and (ii) coincides with the infimum or the supremum, respectively.
In terms of our optimization problem, we will be looking for the maximum of the set of attainable values of ![]() under the constraints of the problem
under the constraints of the problem ![]() :
:
![]()
Now, next to the maximum attainable value, we are frequently also (most of the time: even more) interested in the (set of) solution(s), i.e. the arguments ![]() that maximize
that maximize ![]() under the constraints of
under the constraints of ![]() . So, let’s define them in a next step:
. So, let’s define them in a next step:
Definition: Local and Global Maximizers.
Let ![]() ,
, ![]() . Then,
. Then, ![]() is
is
Verbally, local means that there must be a neighborhood (i.e. an open ball ![]() around
around ![]() , restricted to the domain
, restricted to the domain ![]() of
of ![]() to ensure that
to ensure that ![]() is defined for every considered argument) such that
is defined for every considered argument) such that ![]() maximizes
maximizes ![]() in this neighborhood, or respectively, it maximizes the restricted function
in this neighborhood, or respectively, it maximizes the restricted function
![]()
Strict means that ![]() is the unique maximizer of
is the unique maximizer of ![]() (local: when restricted to a neighborhood), such that all other
(local: when restricted to a neighborhood), such that all other ![]() (in this neighborhood) yield strictly lower values for
(in this neighborhood) yield strictly lower values for ![]() if
if ![]() is defined in
is defined in ![]() , i.e.
, i.e. ![]() . Note that local implies global, because if all elements of
. Note that local implies global, because if all elements of ![]() yield smaller values for
yield smaller values for ![]() than
than ![]() , then so do especially all those that lie in neighborhoods of
, then so do especially all those that lie in neighborhoods of ![]() . The converse is not always true, and some local maximizers may not be global ones.
. The converse is not always true, and some local maximizers may not be global ones.
In optimization, infrequently care about the whole set ![]() , as it contains many points that do not satisfy the given constraints. Let us see how we can formally restrict the problem to only those points consistent with the problem’s constraints:
, as it contains many points that do not satisfy the given constraints. Let us see how we can formally restrict the problem to only those points consistent with the problem’s constraints:
Definition: Restriction of a Function.
Let ![]() be sets and
be sets and ![]() a function. Then, for
a function. Then, for ![]() , the function
, the function ![]() is called the restriction of
is called the restriction of ![]() on
on ![]() .
.
Definition: Constraint Set.
Consider an optimization problem ![]() with objective function
with objective function ![]() ,
, ![]() , equality constraints
, equality constraints ![]()
![]() and inequality constraints
and inequality constraints ![]()
![]() . Then, the set
. Then, the set
![]()
is called the constraint set of ![]() .
.
The constraint set of a problem ![]() defines the restriction
defines the restriction ![]() . Beyond now being able to represent optimization problems more compactly as
. Beyond now being able to represent optimization problems more compactly as
![]()
the value of having defined the constraint set is that it more formally narrows down what we are indeed after when considering the problem ![]() mathematically: finding the maximizers of the restricted function
mathematically: finding the maximizers of the restricted function ![]() ! Note that for an unconstrained problem, we simply have
! Note that for an unconstrained problem, we simply have ![]() so that
so that ![]() . Beyond the general maximizers defined above, this allows us to define the maximizers we care about in optimization problems:
. Beyond the general maximizers defined above, this allows us to define the maximizers we care about in optimization problems:
Definition: Solutions, Maximizing Arguments.
Consider an optimization problem ![]() with constraint set
with constraint set ![]() . The solutions to
. The solutions to ![]() are given by the set of global maximizers of
are given by the set of global maximizers of ![]() ,
,
![]()
We call ![]() the maximizing arguments or the arg max of the problem
the maximizing arguments or the arg max of the problem ![]() . If this set contains only a single element
. If this set contains only a single element ![]() , we also write
, we also write ![]() .
.
As indicated by the bold words, it is crucial to note that the solutions typically constitute a set that may contain arbitrarily many elements or none at all (consider e.g. ![]() or
or ![]() ). Only if there is a unique maximizer, by convention, the arg max also refers to a number or a vector (but still to the set as well)! Finally, note that regardless of whether the problem
). Only if there is a unique maximizer, by convention, the arg max also refers to a number or a vector (but still to the set as well)! Finally, note that regardless of whether the problem ![]() has solutions, and even regardless of whether there are any values that satisfy the constraints (i.e., whether
has solutions, and even regardless of whether there are any values that satisfy the constraints (i.e., whether ![]() ), the arg max is always defined!
), the arg max is always defined!
Now that we have introduced all key concepts of the optimization context, it is a good time to make sure that we are thoroughly familiar with them. To practice, consider these two objects that you frequently see across all economic fields, and applications of mathematics more generally:
![]()
Try to answer the following questions on their differences and their relationship:
In doing so, be aware that the former expression is shorthand notation for ![]() .
.
For this subsection, make sure to recall the concepts of (i) a bounded set, (ii) a closed set, (iii) supremum and infimum, and (iv) the Heine-Borel theorem for characterization of compactness in ![]() that have been introduced throughout the earlier chapters of this script.
that have been introduced throughout the earlier chapters of this script.
First, we need one more definition:
Definition: Bounded Function.
Let ![]() be a real-valued function. If
be a real-valued function. If ![]() , the image of
, the image of ![]() under
under ![]() is bounded, we say that
is bounded, we say that ![]() is a bounded function. Moreover, for
is a bounded function. Moreover, for ![]() , we say that
, we say that ![]() is bounded on
is bounded on ![]() if
if ![]() is bounded.
is bounded.
Recall that when discussing Heine-Borel, we highlighted the value of compact subsets of ![]() for optimization: a continuous function will necessarily assume both a (global) maximum and minimum on them, such that compactness of the set is a sufficient condition for existence of solutions to optimization problems! To transfer this intuition to the
for optimization: a continuous function will necessarily assume both a (global) maximum and minimum on them, such that compactness of the set is a sufficient condition for existence of solutions to optimization problems! To transfer this intuition to the ![]() , we need to review what Heine-Borel precisely says about compact sets: they are closed and bounded. Boundedness of a set
, we need to review what Heine-Borel precisely says about compact sets: they are closed and bounded. Boundedness of a set ![]() , defined as
, defined as ![]() being contained in some ball
being contained in some ball ![]() where
where ![]() and
and ![]() is immensely helpful because it restricts the degree to which the arguments
is immensely helpful because it restricts the degree to which the arguments ![]() of a function
of a function ![]() can extend into any direction in
can extend into any direction in ![]() — if they move too far away from
— if they move too far away from ![]() , then boundedness tells us that they can no longer be arguments of
, then boundedness tells us that they can no longer be arguments of ![]() ! Similar to the univariate case where bounded sets are intervals with finite bounds, this prevents solution-breakers like limits
! Similar to the univariate case where bounded sets are intervals with finite bounds, this prevents solution-breakers like limits ![]() , as e.g. in
, as e.g. in ![]() where if x is allowed to infinitely expand e.g. in direction
where if x is allowed to infinitely expand e.g. in direction ![]() , then it is allowed to diverge to
, then it is allowed to diverge to ![]() as
as ![]() . As with univariate functions, we can prevent this by defining
. As with univariate functions, we can prevent this by defining ![]() on a bounded set. Next, why do we need closedness? For univariate functions, this is also rather straightforward: if e.g.
on a bounded set. Next, why do we need closedness? For univariate functions, this is also rather straightforward: if e.g. ![]() , then the set is bounded and
, then the set is bounded and ![]() can not diverge due to “too large” arguments, but clearly, for any
can not diverge due to “too large” arguments, but clearly, for any ![]() , and since the domain of
, and since the domain of ![]() does not include its boundary, there are neither minimizing nor maximizing values! This logic extends to the multivariate case in a one-to-one fashion.
does not include its boundary, there are neither minimizing nor maximizing values! This logic extends to the multivariate case in a one-to-one fashion.
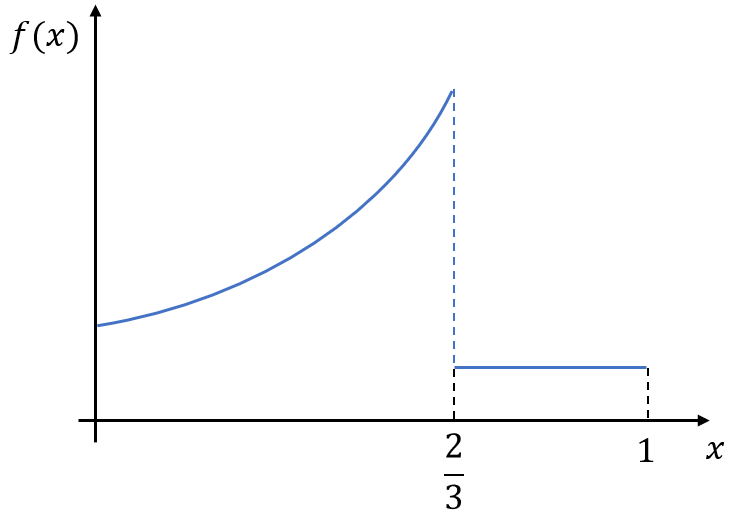
Finally, why do we need continuity? To see this, consider the function
![Rendered by QuickLaTeX.com \[ f:[0,1]\mapsto\mathbb R, x\mapsto f(x) = \begin{cases} x^2 + 2 & x<2/3 \\ 1 & 1\geq 2/3\end{cases}\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-a413675032db213654cd1a02fd9f8576_l3.png)
the graph of which is illustrated in the figure above. What is the maximizer of ![]() ? Clearly, it is not an element of
? Clearly, it is not an element of ![]() , so we can restrict our search to
, so we can restrict our search to ![]() . But this set is no longer closed, and we may run into our boundary problem again — and the way
. But this set is no longer closed, and we may run into our boundary problem again — and the way ![]() is defined, we indeed do! More generally, if
is defined, we indeed do! More generally, if ![]() is discontinuous, the function can “jump”, i.e. it can increase or decrease steadily into one direction, but just before reaching the high/low point, attain an entirely different value. In other words, when
is discontinuous, the function can “jump”, i.e. it can increase or decrease steadily into one direction, but just before reaching the high/low point, attain an entirely different value. In other words, when ![]() approaches
approaches ![]() , it approaches the level
, it approaches the level ![]() . If this level would be a maximum/minimum, we need to ensure that it lies in the range of
. If this level would be a maximum/minimum, we need to ensure that it lies in the range of ![]() by requiring
by requiring ![]() , which is precisely the definition of continuity.
, which is precisely the definition of continuity.
It is possible to show formally that the intuitive line of reasoning above goes through formally:
Theorem: Weierstrass Extreme Value Theorem.
Suppose that ![]() is compact, and that
is compact, and that ![]() is continuous, then,
is continuous, then, ![]() assumes its maximum and minimum on
assumes its maximum and minimum on ![]() , such that
, such that ![]() and
and ![]() .
.
As per our tradition of moving from easier to harder problems, we begin the study of optimization problems with those that are not subject to any constraints, but just seek to maximize a function ![]() over its domain, i.e.
over its domain, i.e.
![]()
where dom![]() and
and ![]() is a real-valued function. From a technical side, note that when considering constrained problems, we may equivalently consider the “unconstrained” problem with objective
is a real-valued function. From a technical side, note that when considering constrained problems, we may equivalently consider the “unconstrained” problem with objective ![]() , but the key complication is that continuity of
, but the key complication is that continuity of ![]() and appealing properties of the domain do not transfer easily to this issue, such that we need to consider it later on its own right.
and appealing properties of the domain do not transfer easily to this issue, such that we need to consider it later on its own right.
To solve optimization problems, we typically rely on a combination of necessary and sufficient conditions. Here, we focus on the perhaps most commonly known conditions: the first and second order necessary conditions for a local extremizer.
For univariate functions ![]() ,
, ![]() , you may know how to approach the problem of unconstrained optimization: set the first derivative of
, you may know how to approach the problem of unconstrained optimization: set the first derivative of ![]() to zero, and check that the second derivative is smaller than
to zero, and check that the second derivative is smaller than ![]() — any point that satisfies these conditions is a candidate for an interior solution. Next to the interior solutions, you will have to consider border solutions: points of non-differentiability and points on the boundary of the support
— any point that satisfies these conditions is a candidate for an interior solution. Next to the interior solutions, you will have to consider border solutions: points of non-differentiability and points on the boundary of the support ![]() of
of ![]() . There are, of course, applications where you need not worry about border solutions: if
. There are, of course, applications where you need not worry about border solutions: if ![]() is differentiable everywhere (especially:
is differentiable everywhere (especially: ![]() , so that the second derivative is easily computed) or the boundary points are either non-existent (
, so that the second derivative is easily computed) or the boundary points are either non-existent (![]() ) or excluded from the domain (
) or excluded from the domain (![]() ). Either way, you evaluate
). Either way, you evaluate ![]() at all candidate points that you found, and the one yielding the highest value is your global maximizer. Here, we focus on how this procedure extends to the multivariate context.
at all candidate points that you found, and the one yielding the highest value is your global maximizer. Here, we focus on how this procedure extends to the multivariate context.
First of all, it is noteworthy that we restrict attention to local maximizers in our analytical search, and only subsequently identify the global maximum from the rather crude and inelegant technique of comparing the value of the objective at all candidates. To find necessary conditions, we restrict attention to the interior, the (finite set of) boundary points are considered in isolation subsequently! Note that we assume away the non-differentiability issue by imposing ![]() , otherwise, we would worry about these points too.
, otherwise, we would worry about these points too.
To come up with the necessary conditions we use, we imagine for the moment that there is a point ![]() that maximizes
that maximizes ![]() locally, and search for some (ideally strong) characteristic features
locally, and search for some (ideally strong) characteristic features ![]() must necessarily have. Starting from the univariate case, suppose
must necessarily have. Starting from the univariate case, suppose ![]() is a local maximizer, such that for the
is a local maximizer, such that for the ![]() -ball restricted to
-ball restricted to ![]() with
with ![]() , there are no values of
, there are no values of ![]() above
above ![]() , i.e.
, i.e. ![]() . Then, how does
. Then, how does ![]() look like around
look like around ![]() , provided that it is (twice) differentiable and thus especially continuous?
, provided that it is (twice) differentiable and thus especially continuous?
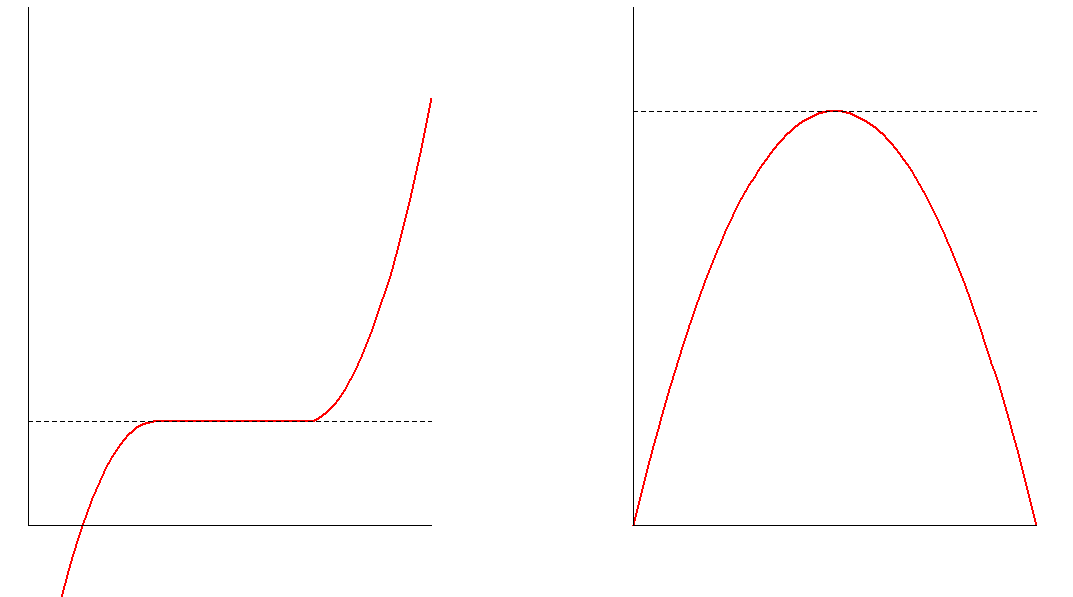
As you can see, ![]() must either be flat around
must either be flat around ![]() , or constitute a “hill” with peak
, or constitute a “hill” with peak ![]() (a mixture also exists, with flatness on one side and a “downhill” part on the other). What does this mean? As illustrated, intuitively, we should have a zero slope of
(a mixture also exists, with flatness on one side and a “downhill” part on the other). What does this mean? As illustrated, intuitively, we should have a zero slope of ![]() at
at ![]() , or for a multivariate function
, or for a multivariate function ![]() , a zero gradient, i.e. a zero slope into any direction (generalizing the concepts of flatness and hilltop to the
, a zero gradient, i.e. a zero slope into any direction (generalizing the concepts of flatness and hilltop to the ![]() ). Indeed, this intuition holds formally:
). Indeed, this intuition holds formally:
Theorem: Unconstrained Interior Maximum – First Order Necessary Condition.
Let ![]() and
and ![]() . Suppose that
. Suppose that ![]() is a local maximizer of
is a local maximizer of ![]() . Then,
. Then, ![]() .
.
The intuition for the formal reason behind this theorem is easy to see from the univariate case: recall that a differentiable function ![]() was strictly increasing (decreasing) in
was strictly increasing (decreasing) in ![]() if and only if
if and only if ![]() , and because
, and because ![]() is twice differentiable,
is twice differentiable, ![]() is differentiable and thus especially continuous. Thus, if
is differentiable and thus especially continuous. Thus, if ![]() , (
, (![]() ), by continuity,
), by continuity, ![]() (
(![]() ) for points “close enough” to
) for points “close enough” to ![]() , and thus, there lie points slightly to the right (left) of
, and thus, there lie points slightly to the right (left) of ![]() with strictly larger values, and
with strictly larger values, and ![]() can not be a maximizer! Thus,
can not be a maximizer! Thus, ![]() can not be a local maximizer unless
can not be a local maximizer unless ![]() – which gives the necessary condition. For the multivariate case, this reasoning applies along any of the fundamental directions of the domain, which involves slightly more notation, but the principle is the same.
– which gives the necessary condition. For the multivariate case, this reasoning applies along any of the fundamental directions of the domain, which involves slightly more notation, but the principle is the same.
The theorem above suggests that points with a zero gradient are important. Indeed, they deserve an own label:
Definition: Critical Point or Stationary Point.
Let ![]() ,
, ![]() and
and ![]() . Then, if
. Then, if ![]() is differentiable at
is differentiable at ![]() and
and ![]() , we call
, we call ![]() a critical point of
a critical point of ![]() or a stationary point of
or a stationary point of ![]() .
.
Note that just because we have defined generally, a critical point need not exist in every specific scenario! There are a broad variety of functions that have a non-zero gradient everywhere, e.g. ![]() , just like there are univariate functions with a globally non-zero derivative. Also, it is easily seen that this condition is not sufficient for a local maximizer, because
, just like there are univariate functions with a globally non-zero derivative. Also, it is easily seen that this condition is not sufficient for a local maximizer, because ![]() applies also to local minima that are not local maxima. Accordingly, the first order necessary condition is the same for local minima and maxima! Moreover,
applies also to local minima that are not local maxima. Accordingly, the first order necessary condition is the same for local minima and maxima! Moreover, ![]() applies to “saddle points”, as illustrated in the left panel of the figure above, which are neither local minima nor maxima.
applies to “saddle points”, as illustrated in the left panel of the figure above, which are neither local minima nor maxima.
As has just emerged, the distinction between local maxima and minima lies beyond the first derivative. Thus, it is generally not sufficient to set the first derivative to zero when looking for a maximum! But as you know, we can consult the second derivative to tell maximizers and minimizers apart. To find a further helpful necessary condition, our thought experiment is again to start from a local maximizer and think about a property it necessary satisfies.
To see the intuition, consider again the univariate case: if ![]() is a local maximizer of
is a local maximizer of ![]() , in a small-enough neighborhood around
, in a small-enough neighborhood around ![]() , there can be no points
, there can be no points ![]() so that
so that ![]() . Accordingly, it must necessarily be the case that
. Accordingly, it must necessarily be the case that ![]() to the left and
to the left and ![]() to the right of
to the right of ![]() – or respectively,
– or respectively, ![]() must be a decreasing function around
must be a decreasing function around ![]() . Because
. Because ![]() is differentiable, we can express this notion using its derivative
is differentiable, we can express this notion using its derivative ![]() : in a neighborhood of
: in a neighborhood of ![]() , we must have that
, we must have that ![]() . To extend this to the multivariate case, recall that matrix definiteness can be viewed as a generalization of the sign, so that the second derivative of a multivariate function, its Hessian, is “smaller or equal to zero” if it is negative semi-definite. Indeed, it formally holds that:
. To extend this to the multivariate case, recall that matrix definiteness can be viewed as a generalization of the sign, so that the second derivative of a multivariate function, its Hessian, is “smaller or equal to zero” if it is negative semi-definite. Indeed, it formally holds that:
Theorem: Unconstrained Interior Maximum — Second Order Necessary Condition.
Let ![]() and
and ![]() . Suppose that
. Suppose that ![]() is a local maximizer of
is a local maximizer of ![]() . Then, if
. Then, if ![]() is twice continuously differentiable at
is twice continuously differentiable at ![]() ,
, ![]() is negative semi-definite.
is negative semi-definite.
Similarly, for a local minimum, we can of course invert the logic of our intuitive reasoning above. This suggests:
Theorem: Unconstrained Interior Minimum — Second Order Necessary Condition.
Let ![]() and
and ![]() . Suppose that
. Suppose that ![]() is a local minimizer of
is a local minimizer of ![]() . Then, if
. Then, if ![]() is twice continuously differentiable at
is twice continuously differentiable at ![]() ,
, ![]() is positive semi-definite.
is positive semi-definite.
Indeed, also the formal reasoning behind the second order necessary condition for the minimum is exactly analogous to the one for the maximum.
One can nicely illustrate the grasp of this necessary condition by illustrating critical values of bivariate functions it rules out: consider ![]() . The necessary condition of a critical point tells us that any candidate
. The necessary condition of a critical point tells us that any candidate ![]() must satisfy
must satisfy
![]()
Thus, there is a unique candidate… But is it also a maximizer (or minimizer)? Let’s consult the Hessian — it is straightforward to verify that for all ![]() ,
,
![]()
What about its definiteness? Pick ![]() . Then,
. Then,
![]()
Thus, there exist ![]() and
and ![]() such that
such that
![]()
and ![]() is neither positive nor negative semi-definite, i.e. it is indefinite. Thus, the solution
is neither positive nor negative semi-definite, i.e. it is indefinite. Thus, the solution ![]() can neither constitute a local maximum nor a local minimum: we call this a saddle point. To see why, consult the figure below, and think how this would fit on a horse (or your preferred animal to ride).
can neither constitute a local maximum nor a local minimum: we call this a saddle point. To see why, consult the figure below, and think how this would fit on a horse (or your preferred animal to ride).
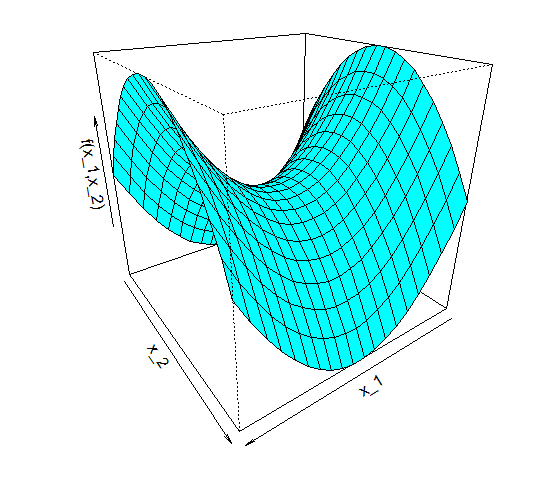
The crucial thing to take away from multivariate saddle points is that the critical value constitutes a maximum in one direction (here: ![]() , i.e. moving along the
, i.e. moving along the ![]() -axis) but a minimum in the other (
-axis) but a minimum in the other (![]() ).
).
Also, it is important to know that this condition is indeed only necessary – it still applies to more points than we would ideally hope for, and even combining both necessary conditions introduced above, we still find points that are no local extremizers. To see this in an example, consider ![]() :
:
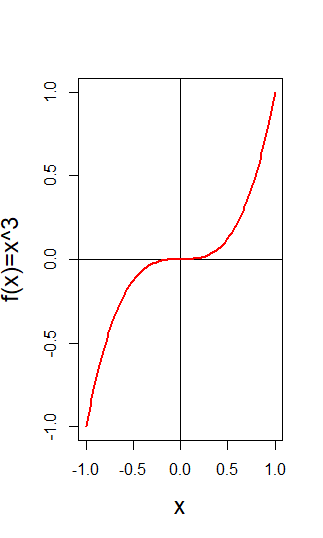
Clearly, the function has a saddle point at ![]() . Since
. Since ![]() and
and ![]() , we get the unique critical value at
, we get the unique critical value at ![]() with second derivative
with second derivative ![]() , which is indeed negative semi-definite! Therefore, both necessary conditions for a local maximum hold at this point. However, so does the positive semi-definiteness condition for the local minimum. The graph will ensure you that the point is neither:
, which is indeed negative semi-definite! Therefore, both necessary conditions for a local maximum hold at this point. However, so does the positive semi-definiteness condition for the local minimum. The graph will ensure you that the point is neither: ![]() for any
for any ![]() , the function strictly increases (decreases) in value for infinitely small deviations to the right (left) of
, the function strictly increases (decreases) in value for infinitely small deviations to the right (left) of ![]() . Thus, both the first and second order necessary conditions hold, but we don’t have a maximum (or a minimum). Hence, we need more conditions to rule out points like
. Thus, both the first and second order necessary conditions hold, but we don’t have a maximum (or a minimum). Hence, we need more conditions to rule out points like ![]() in the example here, and ideally this time sufficient ones that leave no room for critical points that are not the type of local extremum we want to find.
in the example here, and ideally this time sufficient ones that leave no room for critical points that are not the type of local extremum we want to find.
Continuing our intuitive investigations into the univariate case, we can indeed strengthen our requirements imposed on the second derivative to get a sufficient condition. Above, we said that around a local maximum, ![]() must be decreasing, a notion that also allows
must be decreasing, a notion that also allows ![]() to be constant. However, if it is not, i.e. if
to be constant. However, if it is not, i.e. if ![]() and
and ![]() is strictly decreasing around
is strictly decreasing around ![]() , then we know that any point in a small-enough neighborhood of
, then we know that any point in a small-enough neighborhood of ![]() will lead to strictly smaller values of the objective
will lead to strictly smaller values of the objective ![]() – and in such cases,
– and in such cases, ![]() always constitutes a strict local maximizer! From the word “always”, you can immediately see that the condition considered will be sufficient. To generalize to the multivariate case, we again rely on the intuitive link between the sign of a scalar second derivative and the definiteness of a matrix valued one.
always constitutes a strict local maximizer! From the word “always”, you can immediately see that the condition considered will be sufficient. To generalize to the multivariate case, we again rely on the intuitive link between the sign of a scalar second derivative and the definiteness of a matrix valued one.
Note that we only strengthened the second order condition; the first order necessary condition, i.e. ![]() being a critical point, must still be imposed separately. This gives:
being a critical point, must still be imposed separately. This gives:
Theorem: Unconstrained Interior Strict Local Maximum — Sufficient Conditions.
Let ![]() ,
, ![]() and
and ![]() . Suppose that
. Suppose that ![]() is a critical point of
is a critical point of ![]() , and that
, and that ![]() is negative definite. Then,
is negative definite. Then, ![]() is a strict local maximizer of
is a strict local maximizer of ![]() .
.
Again, analogous reasoning can be applied to obtain the corresponding theorem for the minimum:
Theorem: Unconstrained Interior Strict Local Minimum — Sufficient Conditions.
Let ![]() ,
, ![]() and
and ![]() . Suppose that
. Suppose that ![]() is a critical point of
is a critical point of ![]() , and that
, and that ![]() is positive definite. Then,
is positive definite. Then, ![]() is a strict local minimizer of
is a strict local minimizer of ![]() .
.
While the necessary condition was not sufficiently restrictive to find only local maxima, the sufficient condition faces the converse issue: while it only finds local maxima, it may be even too restrictive to find all of them! This needs to be taken into account when coming up with our solution technique below.
Now that we have established the sufficient condition for a local interior maximum, let us take a moment to think about what to make of the results thus far. Indeed, we are ready to discuss the general approach to solving unconstrained optimization problems. When concerned with interior maxima, we can restrict the candidate set to critical values, because all potential maxima are necessarily critical values! Then, if ![]() is “sufficiently smooth” (i.e., it satisfies all required differentiability conditions — here: being twice continuously differentiable at all critical values) we can check the Hessian and determine its definiteness. If at a critical value
is “sufficiently smooth” (i.e., it satisfies all required differentiability conditions — here: being twice continuously differentiable at all critical values) we can check the Hessian and determine its definiteness. If at a critical value ![]() ,
, ![]() is negative (positive) definite, we have sufficient evidence that
is negative (positive) definite, we have sufficient evidence that ![]() is a local maximum (minimum)! That may not be necessary — but we can rule out any value
is a local maximum (minimum)! That may not be necessary — but we can rule out any value ![]() where
where ![]() is not at least negative (positive) semi-definite, because they violate the necessary conditions. Thus, we are generally happy if all critical values are associated with either a positive/negative definite Hessian or an indefinite one — but we have to beware semi-definite Hessians, for which no theorem tells us whether or not such points are extrema! As a further note of caution, all theorems thus far have concerned interior points — for boundary points, no theorem exists, and we must either consider them in isolation or simply consider
is not at least negative (positive) semi-definite, because they violate the necessary conditions. Thus, we are generally happy if all critical values are associated with either a positive/negative definite Hessian or an indefinite one — but we have to beware semi-definite Hessians, for which no theorem tells us whether or not such points are extrema! As a further note of caution, all theorems thus far have concerned interior points — for boundary points, no theorem exists, and we must either consider them in isolation or simply consider ![]() with an open set
with an open set ![]() such that the boundary issue is avoided altogether, which, however, may prevent us to argue for solution existence using the Weierstrass theorem (as typically, an open set is either not closed or not bounded).
such that the boundary issue is avoided altogether, which, however, may prevent us to argue for solution existence using the Weierstrass theorem (as typically, an open set is either not closed or not bounded).
Accordingly, the consideration of the Hessian function helps us to categorize all our candidates – the critical points solving the first order condition plus “border solutions” – into the following categories:

The last two colums indicate whether we keep the respective point in the set of candidates for which we compare values in the final step when searching for a global maximum, and why (or why not). Note that indefinite and positive definite Hessians are special cases of Hessians that are not negative definite. The reason that they are listed separately is that we can derive a destinctive characterization from the conditions we discussed.
Now, we know the final set of candidates for which we know, or can not rule out, that they constitute a local maximum. In the last step, it remains to evaluate the function at all these points and see which point yields the largest value to conclude on the global maximum. When doing so, one thing has to be kept in mind: we need some justification that the local maximum we found indeed constitutes a global maximum, that is, that the global maximum does indeed exist (in which case, recall, it will definitely be also a local maximum). This is not ex ante guaranteed! In most cases, we can establish this either through the Weierstrass theorem, or by considering the limit behavior of the function – in the multivariate context, along any of its (fundamental) directions. More details can be found in the script.
To see the intuition in the univariate case, consider
![]()
Here, the only critical point is ![]() , where
, where ![]() . Thus, we identify the point as a strict local maximum per our conditions. Since
. Thus, we identify the point as a strict local maximum per our conditions. Since ![]() , the only boundary point here,
, the only boundary point here, ![]() , can be ruled out as the global maximum. Still, ex ante, it is not guaranteed that
, can be ruled out as the global maximum. Still, ex ante, it is not guaranteed that ![]() , which we have to additionally establish to argue for the global maximum. This is straightforward here, since
, which we have to additionally establish to argue for the global maximum. This is straightforward here, since
![]()
where the last equality follows from the quotient rule of the limit.
If instead, the function had been defined as
![]()
we knew that the global maxiumum must exist by the Weierstrass theorem (closed intervals of ![]() are compact), and here, it is sufficient to compare the interior solution
are compact), and here, it is sufficient to compare the interior solution ![]() with the boundary points, i.e.
with the boundary points, i.e. ![]() to
to ![]() and
and ![]() .
.
In summary, we can summarize our approach to finding the global maximizer as follows:
Algorithm: Solving the Unconstrained Maximization Problem.
Indeed, strictly speaking, this “cookbook recipe” for the solution of the unconstrained problem is everything you need to know in practice, and many undergraduate programs indeed teach nothing but this. However, as always, the person knowing the reasons for why some procedure works are much more likely to correctly perform all steps than the one who has only memorized the sequence, especially when things get tricky and non-standard. Also, the correct procedure itself is of course much easier to memorize if you know how it comes to be. Thus, feel encouraged to understand at least the intuition-based elaborations above, if not the formal details outlined in the companion script.
When discussing convexity of functions in the last chapter, we briefly noted that the property is also quite useful for optimization. Let’s see how precisely this is:
Theorem: Sufficiency for the Global Unconstrained Maximum.
Let ![]() be a convex set, and
be a convex set, and ![]() . Then, if
. Then, if ![]() is concave and for
is concave and for ![]() , it holds that
, it holds that ![]() , then
, then ![]() is a global maximizer of
is a global maximizer of ![]() .
.
Analogously, it holds that:
Theorem: Sufficiency for the Global Unconstrained Minimum.
Let ![]() be a convex set, and
be a convex set, and ![]() . Then, if
. Then, if ![]() is convex and for
is convex and for ![]() , it holds that
, it holds that ![]() , then
, then ![]() is a global minimizer of
is a global minimizer of ![]() .
.
The reason for this fact can be seen intuitively again from the univariate case: the second derivative of a concave (convex) function is non-positive (non-negative) everywhere. As such, the first derivative is non-increasing (non-decreasing), and any critical point ![]() will only have points with
will only have points with ![]() (
(![]() ) to its left and only points with
) to its left and only points with ![]() (
(![]() ) to its right. Thus,
) to its right. Thus, ![]() increases (decreases) before the point and decreases thereafter – which defines a global maximum. However, be careful to note that there may be a plateau of global maxima (minima): it is not ruled out that
increases (decreases) before the point and decreases thereafter – which defines a global maximum. However, be careful to note that there may be a plateau of global maxima (minima): it is not ruled out that ![]() remains at
remains at ![]() on some interval in the domain!
on some interval in the domain!
This is extremely powerful: when we have a concave objective function (and many classical economic functions are concave, e.g. most standard utility or production functions), then the critical point criterion (before only necessary for a local maximizer) is now sufficient for a global maximizer! This reduces our multi-step procedure defined in the algorithm above to just looking at the first-order condition, which represents a dramatic reduction in the effort necessary to solve the problem. Thus, it may oftentimes be worthwhile to check convexity and concavity of the objective function in a first step.
If you feel like testing your understanding of the optimization basics and our discussion of unconstrained optimization, you can take a short quiz found here.
Let us take the next step to solving the general optimization problem by now allowing for equality constraints:
![]()
Alternatively, you may read the problem in forms like
![]()
Perhaps, you are familiar with the Lagrangian method — but unless you have had some lectures explicitly devoted to mathematical analysis in your undergraduate studies, I believe you are not familiar with its formal justification, and perhaps also not how we may apply it for multivariate functions. Thus, the following addresses precisely these issues, while restricting attention to the intuition when it comes to the formal details.
Before moving on, make yourself aware that what we are doing here is actually already quite useful in a broad range of applications, since the loss in generality from omitting inequality constraints from the problem formulation, depending on the application in mind, may not be too severe: consider for instance utility maximization with the budget constraint ![]() , meaning that the consumer can not spend more on consumption than his income
, meaning that the consumer can not spend more on consumption than his income ![]() . Now, if there is no time dimension (and thus no savings motive) and he has a utility function
. Now, if there is no time dimension (and thus no savings motive) and he has a utility function ![]() which strictly increases in both arguments, as we typically assume (“strictly more is strictly better”), the consumer will never find it optimal to not spend all his income, so that the problem is entirely equivalent to one with the equality constraint
which strictly increases in both arguments, as we typically assume (“strictly more is strictly better”), the consumer will never find it optimal to not spend all his income, so that the problem is entirely equivalent to one with the equality constraint ![]() !
!
Do you recall our definition of the lower- and upper-level sets when we discussed the generalization of convexity to the multivariate case? Here, we need a closely related concept: the level set, which is both a lower and the upper level set given a certain value!
Definition: Level Set.
Let ![]() ,
, ![]() , and
, and ![]() . Then, we call
. Then, we call ![]() the
the ![]() -level set of
-level set of ![]() .
.
This definition may look indeed familiar, in the sense that you should be able to describe ![]() with vocabulary that has been introduced very early on: think about what we typically would call a set
with vocabulary that has been introduced very early on: think about what we typically would call a set ![]() when
when ![]() is a value in the codomain of
is a value in the codomain of ![]() . As a hint, we denote it by
. As a hint, we denote it by ![]() . … if you have practiced your notation, you will know from this that the level set is nothing but the pre-image of
. … if you have practiced your notation, you will know from this that the level set is nothing but the pre-image of ![]() under
under ![]() ! To see why we care about level sets is analytically straightforward: in our optimization problem, when there is only one constraint
! To see why we care about level sets is analytically straightforward: in our optimization problem, when there is only one constraint ![]() , we are looking for solutions on the level set
, we are looking for solutions on the level set ![]() , i.e.
, i.e. ![]() , in words, the constraint set is nothing but the zero-level set of
, in words, the constraint set is nothing but the zero-level set of ![]() ! With multiple constraints, note that
! With multiple constraints, note that
![Rendered by QuickLaTeX.com \[ \begin{split} C(\mathcal P) &= \{x\in X: g_i(x) = 0\ \forall i\in\{1,\ldots,m\}\} \\& = \{x\in X: (g_1(x) = 0\land g_2(x) = 0\land \ldots \land g_m(x) = 0)\} \\& = \{x\in X: g_1(x) = 0\} \cap \{x\in X: g_2(x) = 0\} \cap \ldots \cap \{x\in X: g_m(x) = 0\} \\&= \bigcap_{i=1}^m L_0(g_i), \end{split}\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-241f8401942b8be38e20bc4222767881_l3.png)
and that we are looking for solutions in the intersections of the level sets.
From a geometrical perspective, level sets are oftentimes useful to map three-dimensional objects onto a two-dimensional space. The most famous practical example is perhaps the one of contour lines as used for geographical maps, as shown below (figure taken from https://www.ordnancesurvey.co.uk/blog/2015/11/map-reading-skills-making-sense-of-contour-lines/, accessed at June 16, 2020):
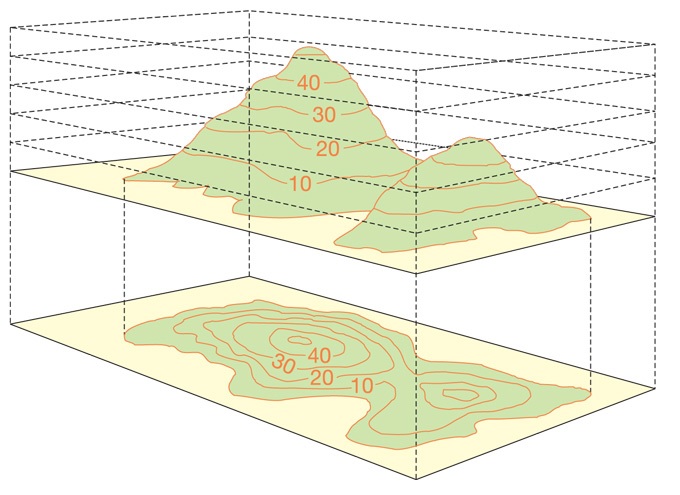
Also in economics, we have various important examples: for instance budget sets (with the restriction that all money is spent) where the level is equal to the disposable income ![]() , and utility functions with level sets
, and utility functions with level sets ![]() for the
for the ![]() . For utility, we usually call sets
. For utility, we usually call sets ![]() indifference sets, and their graphical representation in the
indifference sets, and their graphical representation in the ![]() the indifference curve, which represents all points
the indifference curve, which represents all points ![]() that yield the same utility level
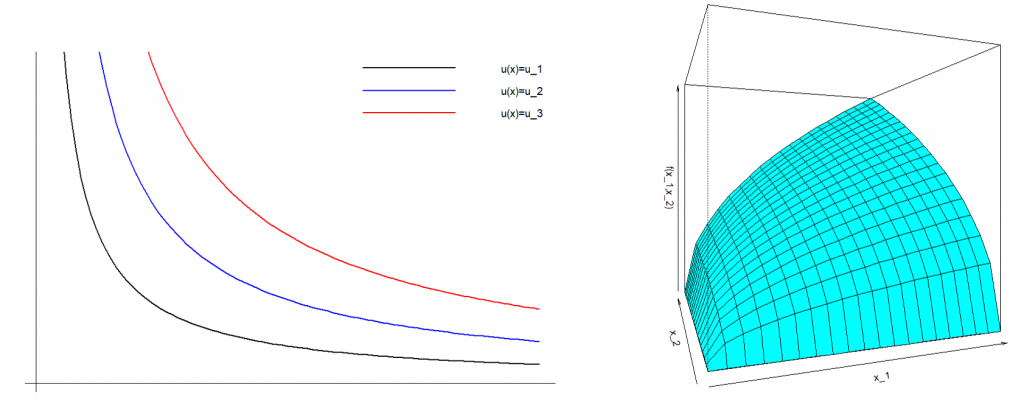
that yield the same utility level ![]() . For the Cobb-Douglas utility with equal coefficients, i.e.
. For the Cobb-Douglas utility with equal coefficients, i.e. ![]() , this relationship is shown here (the RHS plot displays utility on the vertical axis):
, this relationship is shown here (the RHS plot displays utility on the vertical axis):
Coming back to our pre-image interpretation, make sure to understand that one fixes a value of interest, ![]() , that the function may take, for instance either the altitude of a coordinate point, or the utility level associated with a consumption choice. Then, the level set is the collection of all the points
, that the function may take, for instance either the altitude of a coordinate point, or the utility level associated with a consumption choice. Then, the level set is the collection of all the points ![]() that yield this value
that yield this value ![]() when evaluating
when evaluating ![]() at
at ![]() , i.e.
, i.e. ![]() . Note that level sets may just consist of one element, be empty altogether, but conversely may also encompass even the whole domain of
. Note that level sets may just consist of one element, be empty altogether, but conversely may also encompass even the whole domain of ![]() , namely when
, namely when ![]() is a “flat” function.
is a “flat” function.
Now that we have convinced ourselves that equality-constrained maximization is nothing but maximization on level sets, let us think about whether we can use this insight to reduce our new issue of solving the equality-constrained problem to the old one that we already know, the unconstrained problem. There is good news and bad news. The first piece of good news is that precisely this is indeed possible! The (full set of) bad news, however, is that things will get quite heavy in notation. To somewhat mitigate this problem, the following restricts attention to the scenario of one equality constraint — but the generalization entirely works in a one to one fashion, the respective result is given at the end of this section. Finally, the last piece of good news, and perhaps the most re-assuring fact is that while mathematically somewhat tedious to write down, the intuition of the approach is really simple.
To understand how we generally proceed to dealing with equality constrained problems, consider the following simple exemplary problem:
![]()
Our solution approach is to reduce the problem to one without constraints, which we know how to solve from the previous section. The level set that we consider is ![]() for
for ![]() . Here, we can express the condition
. Here, we can express the condition ![]() through an explicit function for
through an explicit function for ![]() with argument
with argument ![]() :
:
![]()
Thus, the constraint indeed fixes ![]() given
given ![]() , and we are only truly free to choose
, and we are only truly free to choose ![]() . Of course, you could also have gone the other way around to express
. Of course, you could also have gone the other way around to express ![]() as a function of
as a function of ![]() ; the key take-away is that the constraint reduces the number of free variables by one. Imposing the restriction of the constraint onto the objective, the problem becomes
; the key take-away is that the constraint reduces the number of free variables by one. Imposing the restriction of the constraint onto the objective, the problem becomes
![]()
The constraint need not be imposed separately, as it has already been plugged in for ![]() and is guaranteed to hold if we set
and is guaranteed to hold if we set ![]() after solving for the optimal
after solving for the optimal ![]() . Thus, being able to plug in the explicit function representing the constraint into the objective has helped us to re-write the problem explicitly as an unconstrained one! If you need practice in unconstrained optimization, go ahead and solve it, as the only local maximizer (which is not a global maximizer because the objective diverges to
. Thus, being able to plug in the explicit function representing the constraint into the objective has helped us to re-write the problem explicitly as an unconstrained one! If you need practice in unconstrained optimization, go ahead and solve it, as the only local maximizer (which is not a global maximizer because the objective diverges to ![]() as
as ![]() ).
).
The issue to transferring this idea to general applications is that coming up with the explicit function, depending on how ![]() looks like, can be prohibitively complex or simply infeasible. In fact, this approach is very unlikely to work outside the context of linear constraints as we have seen it in the example above; already if we introduce square terms, e.g.
looks like, can be prohibitively complex or simply infeasible. In fact, this approach is very unlikely to work outside the context of linear constraints as we have seen it in the example above; already if we introduce square terms, e.g.
![]()
it is no longer possible to solve ![]() for
for ![]() as a function of
as a function of ![]() explicitly, as you arrive at
explicitly, as you arrive at ![]() , that is, two values rather than one that give a value for
, that is, two values rather than one that give a value for ![]() consistent with the constraint given
consistent with the constraint given ![]() , but per our definition of a function, we can have only one value. This is why we need the concept of implicit functions.
, but per our definition of a function, we can have only one value. This is why we need the concept of implicit functions.
To understand the concept of implicit functions, let us think again about why the explicit function was valuable. Starting from a point ![]() in the constraint set
in the constraint set ![]() , when we varied
, when we varied ![]() slightly, we were able to derive an explicit rule on how to adjust
slightly, we were able to derive an explicit rule on how to adjust ![]() in response in order to remain on the level set. That is, when we write the explicit function as
in response in order to remain on the level set. That is, when we write the explicit function as ![]() , for any movement
, for any movement ![]() from
from ![]() , we knew that
, we knew that
![]()
and the point ![]() would also be an element of the level set. So what was the key condition for this to work? Well, we can only “pull
would also be an element of the level set. So what was the key condition for this to work? Well, we can only “pull ![]() back towards
back towards ![]() ” by adjusting
” by adjusting ![]() if the function
if the function ![]() indeed moves with
indeed moves with ![]() , else, the variation in
, else, the variation in ![]() induced by variation in
induced by variation in ![]() can not be counterbalanced by adjustment of
can not be counterbalanced by adjustment of ![]() (e.g. if
(e.g. if ![]() and
and ![]() ). Formally, it is necessary that
). Formally, it is necessary that ![]() . This is precisely the approach we want to generalize now. To be applicable to more general problems, we will weaken the two following strong requirements of the explicit function: (i) being able to derive an explicit mathematical expression for
. This is precisely the approach we want to generalize now. To be applicable to more general problems, we will weaken the two following strong requirements of the explicit function: (i) being able to derive an explicit mathematical expression for ![]() , and (ii) “global” validity of the adjustment rule, that is, applicability to arbitrarily large changes
, and (ii) “global” validity of the adjustment rule, that is, applicability to arbitrarily large changes ![]() . The motivation of (ii) is that we will again be concerned with local extremizers in our search, so that we are already happy with adjustment rules in small neighborhoods of some value for
. The motivation of (ii) is that we will again be concerned with local extremizers in our search, so that we are already happy with adjustment rules in small neighborhoods of some value for ![]() .
.
The intuition above should help understand the rather abstract implicit function theorem presented below. To make it even more accessible, before introducing it, let us re-state the above in terms of a general problem in ![]() arguments, i.e.
arguments, i.e. ![]() and
and ![]() , and think about the conditions that we need to locally express the adjustment in one argument in response to variation in all others necessary to remain on the level set in this context.
, and think about the conditions that we need to locally express the adjustment in one argument in response to variation in all others necessary to remain on the level set in this context.
Suppose that ![]() and
and ![]() are “smooth” in an appropriate sense, for now at least once continuously differentiable, and start from a point
are “smooth” in an appropriate sense, for now at least once continuously differentiable, and start from a point ![]() on the level set
on the level set ![]() . We are looking for a way to express a rule for how to stay on this level set locally, that is, in some neighborhood
. We are looking for a way to express a rule for how to stay on this level set locally, that is, in some neighborhood ![]() of
of ![]() , by defining a function of one variable in all others. Now, suppose that we start from
, by defining a function of one variable in all others. Now, suppose that we start from ![]() and only marginally vary the components at positions
and only marginally vary the components at positions ![]() of
of ![]() , but not the first component, say to
, but not the first component, say to ![]() where
where ![]() and
and ![]() where
where ![]() small. Because
small. Because ![]() is continuous,
is continuous, ![]() should still lie “really close” to
should still lie “really close” to ![]() (
(![]() holds because
holds because ![]() !). By continuous differentiability of
!). By continuous differentiability of ![]() , the first partial derivative of
, the first partial derivative of ![]() is continuous, and we should be able to vary the first argument by
is continuous, and we should be able to vary the first argument by ![]() to move
to move ![]() back to zero, i.e. cancel any potential change in
back to zero, i.e. cancel any potential change in ![]() induced by the marginal variation in the other arguments through a function
induced by the marginal variation in the other arguments through a function ![]() such that
such that
![]()
Of course, we typically need not pick the first element to do this, so that we may instead simply decompose ![]() where
where ![]() is the univariate variable that we want to adjust, and
is the univariate variable that we want to adjust, and ![]() are all the other variables that are allowed to move freely (note that although we write
are all the other variables that are allowed to move freely (note that although we write ![]() , we don’t require
, we don’t require ![]() to be the first element of
to be the first element of ![]() ! You may e.g. have seen this in decompositions like
! You may e.g. have seen this in decompositions like ![]() that says that
that says that ![]() is composed of the
is composed of the ![]() -th element and all other elements). Rather, we can pick any variable for
-th element and all other elements). Rather, we can pick any variable for ![]() that is able to induce variation in
that is able to induce variation in ![]() in a neighborhood of
in a neighborhood of ![]() , i.e. any
, i.e. any ![]() with
with ![]() , as by continuity of
, as by continuity of ![]() ‘s partial derivatives, this is sufficient to ensure that
‘s partial derivatives, this is sufficient to ensure that ![]() will remain non-zero in some small neighborhood
will remain non-zero in some small neighborhood ![]() around
around ![]() .
.
To complete the theorem, consider one more interesting observation: if we define ![]() for
for ![]() , then around
, then around ![]() , we have
, we have ![]() , so that in the neighborhood we consider,
, so that in the neighborhood we consider, ![]() . Assuming for now that
. Assuming for now that ![]() is differentiable, even though we can not compute
is differentiable, even though we can not compute ![]() itself, we can actually use this to derive an expression for the derivative of
itself, we can actually use this to derive an expression for the derivative of ![]() using the chain rule or respectively, the total derivative of
using the chain rule or respectively, the total derivative of ![]() with respect to
with respect to ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{split} 0 = \frac{d\tilde g}{dz}(z) &= \frac{\partial g}{\partial y}(h(z),z)\frac{d y}{d z}(z) + \frac{\partial g}{\partial z}(h(z),z)\frac{d z}{d z}(z) \\&= \frac{\partial g}{\partial y}(h(z),z) \cdot \nabla h(z) + \frac{\partial g}{\partial z}(h(z),z) \end{split}\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-a6a3b12eb7fda4e88ba20f56cfa089cc_l3.png)
where ![]() denotes the vector of partial derivatives with respect to elements of
denotes the vector of partial derivatives with respect to elements of ![]() of length
of length ![]() , and the second line follows as
, and the second line follows as ![]() is equal to
is equal to ![]() , the identity matrix of dimension
, the identity matrix of dimension ![]() . Re-arranging the expression, noting that
. Re-arranging the expression, noting that ![]() is a non-zero real number around
is a non-zero real number around ![]() and we can thus divide by it, we get
and we can thus divide by it, we get
![]()
Finally, we are ready to put everything together by stating the result justifying our approach above:
Theorem: Univariate Implicit Function Theorem.
Let ![]() ,
, ![]() and
and ![]() , and
, and ![]() . Suppose that
. Suppose that ![]() , and that for a
, and that for a ![]() ,
, ![]() . Then, if
. Then, if ![]() , there exists an open set
, there exists an open set ![]() such that
such that ![]() and
and ![]() for which
for which ![]() and
and ![]() . Moreover, it holds that
. Moreover, it holds that ![]() with derivative
with derivative
![]()
Hopefully, the elaborations above help you in understanding the rather abstract statement of this theorem. The next section sheds light on how we end up using it for our optimization context.
The idea that we employ to make use of the implicit function theorem in our constrained optimization context is the following: we consider again a local maximizer as the starting point and contemplate how to characterize it, first through necessary conditions. For this, we locally re-write the constrained problem to an unconstrained one by making use of the implicit function. So, let us focus again on a local maximizer ![]() , this time of the constrained problem
, this time of the constrained problem
![]()
This means that ![]() and for an
and for an ![]() , for any
, for any ![]() ,
, ![]() . If we now meet the requirement of the implicit function theorem, i.e.
. If we now meet the requirement of the implicit function theorem, i.e. ![]() , then we can define our implicit function
, then we can define our implicit function ![]() , for which especially
, for which especially ![]() , and we also have a
, and we also have a ![]() such that:
such that:
![]()
Don’t worry too much about the ![]() here, it is certainly
here, it is certainly ![]() , and represents the room of variation left for
, and represents the room of variation left for ![]() when imposing that
when imposing that ![]() and simultaneously that
and simultaneously that ![]() . The important message of this statement is that if
. The important message of this statement is that if ![]() is a local maximizer in the constrained problem and
is a local maximizer in the constrained problem and ![]() , then
, then ![]() is a local maximizer in the unconstrained problem
is a local maximizer in the unconstrained problem
(1) ![]()
But as a local maximizer in an unconstrained problem, we know how to characterize ![]() through necessary and sufficient conditions from the previous section! Hence, it should be possible to derive the same kind of conditions also for the constrained problem, and it indeed is. The following discusses how this transfer works.
through necessary and sufficient conditions from the previous section! Hence, it should be possible to derive the same kind of conditions also for the constrained problem, and it indeed is. The following discusses how this transfer works.
Let us start with the first order condition: ![]() must be a critical point of
must be a critical point of ![]() where
where ![]() as we already defined above. This means that
as we already defined above. This means that ![]() . To obtain a workable first order condition for the constrained problem from this, we need to get rid of the unknown function
. To obtain a workable first order condition for the constrained problem from this, we need to get rid of the unknown function ![]() . In analogy to the derivation above, this can be achieved by applying the total derivative:
. In analogy to the derivation above, this can be achieved by applying the total derivative:
![]()
Now, we just plug in what we know about ![]() from the implicit function theorem, and use that
from the implicit function theorem, and use that ![]() :
:
![Rendered by QuickLaTeX.com \[\mathbf 0 = \frac{\partial f}{\partial y}(y^*,z^*) \cdot \left [-\left (\frac{\partial g}{\partial y}(y^*,z^*)\right )^{-1}\frac{\partial g}{\partial z}(y^*,z^*)\right ] + \frac{\partial f}{\partial z}(y^*,z^*).\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-8e16d595c1c27df3d52770cf0613561c_l3.png)
Re-arranging terms and plugging in that ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[\mathbf 0 = \frac{\partial f}{\partial z}(x^*)-\left [\frac{\partial f}{\partial y}(x^*) \cdot \left (\frac{\partial g}{\partial y}(x^*)\right )^{-1}\right ]\frac{\partial g}{\partial z}(x^*) =: \frac{\partial f}{\partial z}(x^*) - \lambda \frac{\partial g}{\partial z}(x^*)\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-1eb246da7d20bad057643a03092af88b_l3.png)
where we define ![]() as the expression in square brackets. Moreover, it holds that
as the expression in square brackets. Moreover, it holds that
![Rendered by QuickLaTeX.com \[\frac{\partial f}{\partial y}(x^*) - \lambda \frac{\partial g}{\partial y}(x^*) = \frac{\partial f}{\partial y}(x^*) - \left [\frac{\partial f}{\partial y}(x^*) \cdot \left (\frac{\partial g}{\partial y}(x^*)\right )^{-1}\right ] \frac{\partial g}{\partial y}(x^*) = \frac{\partial f}{\partial y}(x^*) - \frac{\partial f}{\partial y}(x^*) = 0.\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-8ed22d91d646fba107e0f33ffb5d807f_l3.png)
Thus, we can summarize more compactly
![]()
This is indeed what we were after: a characterization of the local maximizer ![]() in the constrained problem using first derivatives. Note that this result is an implication of
in the constrained problem using first derivatives. Note that this result is an implication of ![]() being a local maximizer, such that it is a necessary condition for a local maximum. Let us write this down:
being a local maximizer, such that it is a necessary condition for a local maximum. Let us write this down:
Theorem: Lagrange’s Necessary First Order Condition.
Consider the constrained problem ![]() where
where ![]() and
and ![]() . Let
. Let ![]() and suppose that
and suppose that ![]() . Then,
. Then, ![]() is a local maximizer of the constrained problem only if there exists
is a local maximizer of the constrained problem only if there exists ![]() . If such
. If such ![]() exists, we call it the Lagrange multiplier associated with
exists, we call it the Lagrange multiplier associated with ![]() .
.
The condition “![]() ” ensures that we can find the implicit function to express how we may remain within the level set around
” ensures that we can find the implicit function to express how we may remain within the level set around ![]() . Conversely, this means that in comparison to the unconstrained problem, we need to take care of one more “border solution” candidate: singularities of the level set, i.e. points
. Conversely, this means that in comparison to the unconstrained problem, we need to take care of one more “border solution” candidate: singularities of the level set, i.e. points ![]() where
where ![]() and
and ![]() .
.
Let’s take a moment to consider and formally justify the Lagrangian function, or simply, the Lagrangian. The necessary condition is “![]() “. Thus, for said
“. Thus, for said ![]() , it is an easy exercise to verify that evaluated at
, it is an easy exercise to verify that evaluated at ![]() , the gradient of the following function is equal to
, the gradient of the following function is equal to ![]() :
:
![]()
We call this function the Lagrangian. Importantly, from our considerations in the previous section, the necessary condition for a solution to unconstrained maximization of the Lagrangian is ![]() , which is however equivalent to our necessary condition for the constrained problem we had just derived. Finally, note that the derivative of
, which is however equivalent to our necessary condition for the constrained problem we had just derived. Finally, note that the derivative of ![]() with respect to
with respect to ![]() is just
is just ![]() , and requiring
, and requiring ![]() is thus equivalent to requiring
is thus equivalent to requiring ![]() . Thus, any interior solution candidate in the constrained problem is associated with a
. Thus, any interior solution candidate in the constrained problem is associated with a ![]() so that
so that ![]() is a critical point of the Lagrangian function! However, as a technical comment, as you can convince yourself with the help of the companion script, the Lagrangian function never has maxima or minima, but only saddle points. Thus, be careful not to say that constrained maximization is equivalent to maximization of the Lagrangian, as the Lagrangian has no local maximizers and the latter problem never has a solution!
is a critical point of the Lagrangian function! However, as a technical comment, as you can convince yourself with the help of the companion script, the Lagrangian function never has maxima or minima, but only saddle points. Thus, be careful not to say that constrained maximization is equivalent to maximization of the Lagrangian, as the Lagrangian has no local maximizers and the latter problem never has a solution!
Still, the equivalence of critical points gives the usual Lagrangian first order conditions for a solution ![]() that you may be familiar with:
that you may be familiar with:
![]()
This gives a system of ![]() equations is
equations is ![]() unknowns, representing our starting point for searching our solution candidates of any specific equality-constrained problem with one constraint. In the unconstrained case, we could consult the second derivative to further narrow down the set of candidates we needed to compare, and were able to also find a sufficient condition for local maximizers. Let us see how this generalizes to the constrained case. Doing so, we will confine ourselves to studying the theorem and not care too much how precisely this comes to be.
unknowns, representing our starting point for searching our solution candidates of any specific equality-constrained problem with one constraint. In the unconstrained case, we could consult the second derivative to further narrow down the set of candidates we needed to compare, and were able to also find a sufficient condition for local maximizers. Let us see how this generalizes to the constrained case. Doing so, we will confine ourselves to studying the theorem and not care too much how precisely this comes to be.
Definition: Leading Principal Minor.
Consider a symmetric matrix ![]() . Then, for
. Then, for ![]() , the
, the ![]() -th leading principal minor of
-th leading principal minor of ![]() , or the leading principal minor of
, or the leading principal minor of ![]() of order
of order ![]() is the matrix obtained from eliminating all rows and columns with index above
is the matrix obtained from eliminating all rows and columns with index above ![]() from
from ![]() , i.e. the matrix
, i.e. the matrix ![]() .
.
In words, the ![]() -th leading principal minor of
-th leading principal minor of ![]() corresponds to the upper
corresponds to the upper ![]() block of
block of ![]() . Let’s consider an example. Let
. Let’s consider an example. Let
![Rendered by QuickLaTeX.com \[A = \begin{pmatrix} 1 & 4 & 3 & 2\\ 2 & 0 & 0 & 0\\ 3 & 4 & -1 & -2\\ 0 & 1 & e & \pi \end{pmatrix}.\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-02c3a067bc80083da1252cff102af263_l3.png)
Then, the leading principal minors of order ![]() and
and ![]() , respectively, are
, respectively, are
![Rendered by QuickLaTeX.com \[ M^A_1 = (1),\hspace{0.5cm} M^A_2 = \begin{pmatrix} 1 & 4 \\ 2 & 0 \end{pmatrix},\hspace{0.5cm} M^A_3 = \begin{pmatrix} 1 & 4 & 3 \\ 2 & 0 & 0 \\ 3 & 4 & -1 \end{pmatrix},\hspace{0.5cm} M^A_4 = A. \]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-1c0562e61980f3b296bb44f52d2ccc2e_l3.png)
Because it will important for the theorem, answer the following: what are the last two leading principal minors of ![]() ?
?
The last concept that we need for our “second order condition” is the Bordered Hessian Matrix, given by the Hessian of the Lagrangian function:
![Rendered by QuickLaTeX.com \[H_{\mathcal L}(\lambda, x) = \begin{pmatrix} \frac{\partial^2\mathcal L}{\partial \lambda^2}(\lambda, x) & \frac{\partial^2\mathcal L}{\partial \lambda \partial x}(\lambda, x) \\ \frac{\partial^2\mathcal L}{\partial x\partial \lambda}(\lambda, x) & \frac{\partial^2\mathcal L}{\partial x \partial x'}(\lambda, x)\end{pmatrix} = \begin{pmatrix} 0 & -\nabla g(x) \\ -(\nabla g(x))' & H_f(x) - \lambda H_g(x)\end{pmatrix}\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-06cf32d3fd847eaa9e6b4bbdee20f60a_l3.png)
where ![]() and
and ![]() denote the Hessians of
denote the Hessians of ![]() and
and ![]() , respectively.
, respectively.
Theorem: Sufficient Conditions for the Constrained Problem.
Consider the constrained problem ![]() where
where ![]() and
and ![]() . Let
. Let ![]() and
and ![]() such that
such that ![]() is a critical point of the Lagrangian function, i.e.
is a critical point of the Lagrangian function, i.e. ![]() and
and ![]() . If
. If ![]() is the number of equality constraints, denote by
is the number of equality constraints, denote by ![]() the last
the last ![]() principal minors of
principal minors of ![]() . If
. If
Here, sgn![]() denotes the sign function equal to
denotes the sign function equal to ![]() if
if ![]() , to
, to ![]() for
for ![]() and to
and to ![]() else.
else.
Note that we introduced the variable ![]() to indicate the generalization to multiple constraints. Further, note that (i) here, we only have a second order sufficient, but not a second order necessary condition, so our ability to rule out critical values based on failure of a necessary condition is comparatively limited (this is not too bad, usually, there are not too many critical values anyway) and (ii) as with the second order condition in the unconstrained case, we require the functions
to indicate the generalization to multiple constraints. Further, note that (i) here, we only have a second order sufficient, but not a second order necessary condition, so our ability to rule out critical values based on failure of a necessary condition is comparatively limited (this is not too bad, usually, there are not too many critical values anyway) and (ii) as with the second order condition in the unconstrained case, we require the functions ![]() and
and ![]() to be
to be ![]() , i.e. twice continuously differentiable, such that again, the second order condition is subject to a stronger smoothness regularity. Typically in economic problems, this regularity assumption will be satisfied.
, i.e. twice continuously differentiable, such that again, the second order condition is subject to a stronger smoothness regularity. Typically in economic problems, this regularity assumption will be satisfied.
Finally, note that the search for global maxima, because the level set ![]() is usually not convex, the theorem for the unconstrained case does not transfer, such that a concave objective is not sufficient for the global maximum.
is usually not convex, the theorem for the unconstrained case does not transfer, such that a concave objective is not sufficient for the global maximum.
To get a feeling for the Lagrangian method, before moving on to multiple constraints, let us consider an example here: consider the problem
![]()
That is, we seek the vector with minimum Euclidean length ![]() in the
in the ![]() that satisfies
that satisfies ![]() (for economic context, you may think of the length as a cost function and
(for economic context, you may think of the length as a cost function and ![]() as a production target). How do we approach this issue? First, a trick to get rid of the unwieldy square root; let’s consider the equivalent problem
as a production target). How do we approach this issue? First, a trick to get rid of the unwieldy square root; let’s consider the equivalent problem
![]()
This may always be worthwhile to think about — can you re-write the objective to a simpler expression without changing the solutions? Just remember to plug the solutions into the original objective in the end, then this approach works just fine and may save you a lot of work!
In step zero, we think about points that the Lagrangian method won’t find: boundary points and singularities! However, because ![]() is an open set, boundary points are not an issue. Next, at any
is an open set, boundary points are not an issue. Next, at any ![]() , the gradient of the constraint function
, the gradient of the constraint function ![]() is
is ![]() , such that there are no singularities. Thus, we can restrict attention to critical values as found by the Lagrangian method. Make sure that you always think about this step!
, such that there are no singularities. Thus, we can restrict attention to critical values as found by the Lagrangian method. Make sure that you always think about this step!
In the first step, we look for our candidates using the first order necessary conditions, or the Lagrangian first order conditions (FOCs), given by
![]()
So, let’s compute the gradient of ![]() (the one of
(the one of ![]() , we already took care of above):
, we already took care of above):
![]()
Thus, the Lagrangian FOC for ![]() tells us that
tells us that
![]()
This gives either ![]() or
or ![]() . Considering the FOC for
. Considering the FOC for ![]() , i.e. the constraint, the former case can be ruled out; plugging in the latter gives
, i.e. the constraint, the former case can be ruled out; plugging in the latter gives
![]()
Hence, there is just a unique candidate to consider: ![]() . Let’s consult the second order sufficient condition and see whether we can decide upon the type of extremum: recall the form of the Bordered Hessian above. Computing it for an arbitrary
. Let’s consult the second order sufficient condition and see whether we can decide upon the type of extremum: recall the form of the Bordered Hessian above. Computing it for an arbitrary ![]() gives
gives
![Rendered by QuickLaTeX.com \[ H_{\mathcal L}(\lambda,x) = \begin{pmatrix} 0 & -1 & -1\\ -1 & -2 & 0\\ -1 & 0 & -2\end{pmatrix}. \]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-fa2e6a49d18e6166b5f02801eaf9fa52_l3.png)
Thus, it is the same irrepsective of ![]() and
and ![]() , and we don’t need to plug in our candidate solution
, and we don’t need to plug in our candidate solution ![]() . Now, let’s apply the theorem. We have
. Now, let’s apply the theorem. We have ![]() variables and
variables and ![]() constraints, so
constraints, so ![]() , and indeed, we only have to compute the determinant of the last leading principal minor, so the Bordered Hessian itself. Before doing so, let’s form expectations: the point is (i) a maximum if the determinant’s sign is
, and indeed, we only have to compute the determinant of the last leading principal minor, so the Bordered Hessian itself. Before doing so, let’s form expectations: the point is (i) a maximum if the determinant’s sign is ![]() , i.e.
, i.e. ![]() , (ii) a minimum if the determinant’s sign is
, (ii) a minimum if the determinant’s sign is ![]() , i.e.
, i.e. ![]() , and (iii) may be either of the two, or a saddle point if
, and (iii) may be either of the two, or a saddle point if ![]() .
.
Applying our ![]() determinant rule, all the right-diagonals yield a zero product, while we twice get
determinant rule, all the right-diagonals yield a zero product, while we twice get ![]() on the left-diagonal, such that
on the left-diagonal, such that ![]() , and we have indeed found a maximum!
, and we have indeed found a maximum!
To conclude, ![]() minimizes the Euclidean length of vectors in
minimizes the Euclidean length of vectors in ![]() that satisfy
that satisfy ![]() , and it has length
, and it has length
![]() .
.
To conclude our investigations on the case of one equality constraint, let us focus on some intuition and interpretation of the method. First, for our weird and abstract second order sufficient condition that more or less fell from the sky, there is something intuitive to note about it: the number of principal minors to consider. Recall that the gradient of ![]() ,
, ![]() , was ruled out to have a “row rank deficit”, which for row vectors is a fancy way of saying that they are not zero (generally, a matrix
, was ruled out to have a “row rank deficit”, which for row vectors is a fancy way of saying that they are not zero (generally, a matrix ![]() has a row rank deficit if its rank is below
has a row rank deficit if its rank is below ![]() ; this concept will be important in the multivariate extension below). In general, this means that all constraints in
; this concept will be important in the multivariate extension below). In general, this means that all constraints in ![]() move in independent directions at the solution, in our case of just one constraint, it is sufficient that the function
move in independent directions at the solution, in our case of just one constraint, it is sufficient that the function ![]() moves at all with variation in
moves at all with variation in ![]() around the solution, i.e. we have not included a nonsense constraint such as
around the solution, i.e. we have not included a nonsense constraint such as ![]() , or even worse,
, or even worse, ![]() (also the seemingly smart attempt to re-write inequality constraints using indicator functions, e.g.
(also the seemingly smart attempt to re-write inequality constraints using indicator functions, e.g. ![]() as
as ![]() falls victim to this issue at every point where
falls victim to this issue at every point where ![]() is differentiable). As such, the constraint restricts
is differentiable). As such, the constraint restricts ![]() directions of the
directions of the ![]() in maximization of
in maximization of ![]() , but it leaves free the remaining
, but it leaves free the remaining ![]() , which is exactly the number of leading principal minors that we have to consider! Intuitively, you can think about this in analogy to our discussions of the saddle point graph — we need to rule out that we have a minimum in one and a maximum into the other direction.
, which is exactly the number of leading principal minors that we have to consider! Intuitively, you can think about this in analogy to our discussions of the saddle point graph — we need to rule out that we have a minimum in one and a maximum into the other direction.
The second, and perhaps far more important piece of interpretation concerns the Lagrangian multiplier. Have you ever heard the expression “shadow price of the budget constraint”? Then you may know that we associate it with the Lagrangian multiplier in constrained utility maximization subject to the budget constraint. But what does it mean? Let’s consider a general constraint ![]() , but to ease interpretation, keep in mind that
, but to ease interpretation, keep in mind that ![]() may be the budget and we may have
may be the budget and we may have ![]() as the sum of expenditures on individual goods. Note that given
as the sum of expenditures on individual goods. Note that given ![]() , we can express the optimal solution (assuming for now that it is unique) as
, we can express the optimal solution (assuming for now that it is unique) as ![]() , i.e. it will depend only on the value of
, i.e. it will depend only on the value of ![]() (the budget available) that constrains the problem. Denote
(the budget available) that constrains the problem. Denote ![]() as the objective function’s value at the optimum (the implicit utility function
as the objective function’s value at the optimum (the implicit utility function ![]() ), and let
), and let ![]() be the implicit constraint function (expressing expenditures at the optimum,
be the implicit constraint function (expressing expenditures at the optimum, ![]() ). Then, note that by the chain rule,
). Then, note that by the chain rule,
![]()
and thus
![Rendered by QuickLaTeX.com \[ \lambda = \frac{\frac{d}{dy} F(y)}{\frac{d}{dy} G(y)}\hspace{0.5cm} \left (\lambda = \frac{\frac{d}{dy} U(y)}{\frac{d}{dy} E(y)}\right ).\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-f5d07691366091284080ae233a7d65c3_l3.png)
In case of the utility maximization problem, ![]() tells us the ratio of change in utility and change in expenditures. Because the household always spends all his income (provided that the utility function is strictly increasing in consumption), we have
tells us the ratio of change in utility and change in expenditures. Because the household always spends all his income (provided that the utility function is strictly increasing in consumption), we have ![]() so that
so that ![]() , i.e. it resembles the utility’s responsiveness to increases in
, i.e. it resembles the utility’s responsiveness to increases in ![]() . Hence, we can conversely interpret it as the marginal utility cost of being budget-constrained! For the general problem, the intuition is similar, because if we continue to require
. Hence, we can conversely interpret it as the marginal utility cost of being budget-constrained! For the general problem, the intuition is similar, because if we continue to require ![]() , then trivially
, then trivially ![]() , and we can interpret
, and we can interpret ![]() as the marginal increase in the objective function associated with marginally relaxing the constraint. Note that this means that the multiplier MUST BE non-negative, i.e.
as the marginal increase in the objective function associated with marginally relaxing the constraint. Note that this means that the multiplier MUST BE non-negative, i.e. ![]() ! If
! If ![]() , we are in an interesting special case: here, the constraint does not matter, in the sense that
, we are in an interesting special case: here, the constraint does not matter, in the sense that ![]() is the solution to the unconstrained problem as well.
is the solution to the unconstrained problem as well.
Indeed, this intuition will be crucial when we generalize our insights to inequality constraints: if an inequality constraint “matters”, in the set of ![]() such that
such that ![]() , it constrains our optimization opportunities, then it must be the case that it has a non-zero “cost” in terms of the objective, that is, it is associated with a multiplier unequal to zero, and the constraint is binding at
, it constrains our optimization opportunities, then it must be the case that it has a non-zero “cost” in terms of the objective, that is, it is associated with a multiplier unequal to zero, and the constraint is binding at ![]() in the sense that
in the sense that ![]() . Otherwise, if the
. Otherwise, if the ![]() , we say that the constraint is slack, we could deviate marginally from
, we say that the constraint is slack, we could deviate marginally from ![]() and still satisfy the constraint — it thus seems not to have a value cost for the objective, and must be associated with a multiplier
and still satisfy the constraint — it thus seems not to have a value cost for the objective, and must be associated with a multiplier ![]() . This suggests that when
. This suggests that when ![]() is the multiplier associated with the constraint
is the multiplier associated with the constraint ![]() , we should have an equality of the form
, we should have an equality of the form ![]() , called a complementary slackness condition (think about why this equality encompasses the two cases before). Indeed, next to the constraint holding, this is almost all we need to generalize the method to inequality constraints!
, called a complementary slackness condition (think about why this equality encompasses the two cases before). Indeed, next to the constraint holding, this is almost all we need to generalize the method to inequality constraints!
Consider again the Lagrangian (with constraint ![]() ):
):
![]()
Suppose now that we marginally relax the (budget) constraint, that is, assume that ![]() marginally increases (the household gets more money). Then, note that
marginally increases (the household gets more money). Then, note that
![]()
To conclude our studies of equality-constrained optimization problems, we need to briefly consider the method’s generalization to multiple constraints. There is no need for much discussion, all formal ideas and the intuition transfer from the case of one constraint. The only tricky part in generalization here is the rank condition for the Jacobian of the constraint function ![]() , the intuition of which we have already considered above. The reason for the close-to one-to-one transferability is that when starting from a problem of the form
, the intuition of which we have already considered above. The reason for the close-to one-to-one transferability is that when starting from a problem of the form
![]()
we can always define ![]() as above so that
as above so that
![]()
which looks very much like the constraint set of the one-constraint problem, only that we are now dealing with a vector-valued function that must be equal to the zero vector. But, as you may recall from Chapter 1, vector spaces are endowed with very similar algebraic structures as real numbers, that in many cases, including this one, allow for convenient and relatively straightforward generalizations. Indeed, we may rely on the multivariate implicit function theorem:
Theorem: Multivariate Implicit Function Theorem.
Let ![]() ,
, ![]() and
and ![]() , and
, and ![]() . Suppose that
. Suppose that ![]() , and that for a
, and that for a ![]() ,
, ![]() . Then, if
. Then, if ![]() , there exists an open set
, there exists an open set ![]() such that
such that ![]() and
and ![]() for which
for which ![]() and
and ![]() . Moreover, it holds that
. Moreover, it holds that ![]() with derivative
with derivative
![]()
The important changes from the univariate theorem are underlined. You can see that the only thing that has really changed is the rank condition, which encompasses the univariate case, as when ![]() ,
, ![]() is equivalent to
is equivalent to ![]() , the rest is just adjustment to the increased dimensionality of
, the rest is just adjustment to the increased dimensionality of ![]() . Note that in the general case,
. Note that in the general case, ![]() is the matrix-valued Jacobian. The intuition is the same as before: for every constraint
is the matrix-valued Jacobian. The intuition is the same as before: for every constraint ![]() , we need to vary
, we need to vary ![]() independently from the other constraints so as to ensure that it holds in a neighborhood of the point of interest. As in the univariate case, we can not have
independently from the other constraints so as to ensure that it holds in a neighborhood of the point of interest. As in the univariate case, we can not have ![]() , i.e. more (meaningful) constraints than directions of variation.
, i.e. more (meaningful) constraints than directions of variation.
In analogy to above, this theorem allows us to derive the necessary first order condition that gives us the set of “interior” candidates for extrema:
Theorem: Lagrange’s Necessary First Order Conditions for Multiple Constraints.
Consider the constrained problem ![]() where
where ![]() and
and ![]() . Let
. Let ![]() and suppose that
and suppose that ![]() . Then,
. Then, ![]() is a local maximizer of the constrained problem only if there exists
is a local maximizer of the constrained problem only if there exists ![]() . If such
. If such ![]() exists, we call
exists, we call ![]() the Lagrange multiplier associated with
the Lagrange multiplier associated with ![]() for the
for the ![]() -th constraint.
-th constraint.
Here, instead of ![]() , you may be more familiar with the condition
, you may be more familiar with the condition
![Rendered by QuickLaTeX.com \[\nabla f(x^*) = \sum_{i=1}^m \lambda_i\nabla g_i(x^*).\]](https://e600.uni-mannheim.de/wp-content/ql-cache/quicklatex.com-ebd601310d37164bb59cd776f5a716a9_l3.png)
You can check that these two characterizations are equivalent using the definition of the Jacobian. As before, this theorem gives us all the candidates for local extrema that we have to consider when searching for the global maximum/minimum. As with the univariate case, the ![]() -th multiplier can be interpreted as the (non-negative) value cost of the
-th multiplier can be interpreted as the (non-negative) value cost of the ![]() -th constraint at
-th constraint at ![]() .
.
Ruling out extreme values with the second order necessary condition is exactly analogous to before (because we had already formulated the second order condition quite generally earlier):
Theorem: Second Order Sufficient Conditions for Multiple Constraints.
Consider the constrained problem ![]() where
where ![]() and
and ![]() . Let
. Let ![]() and
and ![]() such that
such that ![]() is a critical point of the Lagrangian function, i.e.
is a critical point of the Lagrangian function, i.e. ![]() and
and ![]() . Denote by
. Denote by ![]() the last
the last ![]() principal minors of
principal minors of ![]() . If
. If
Next to the slightly different first order condition, the only difference is the form of the Bordered Hessian. It still corresponds to the Hessian of the Lagrangian function, however, due to the multitude of constraints, this Hessian now looks slightly different:
![]()
You can try to compute this yourself using the definition of the Hessian and appreciating the vector structure of ![]() . Note again that we need a stronger smoothness assumption for the second order necessary condition, as
. Note again that we need a stronger smoothness assumption for the second order necessary condition, as ![]() and
and ![]() need to be
need to be ![]() .
.
We have done quite some math to establish our approach to equality-constrained problems using the Lagrangian function. Having a good understanding of this analytic justification will greatly aid your general knowledge in econ-related math, however, it may be a bit overwhelming, such that the clear path to approach a specific problem may not be crystal clear just yet. Thus, in our last discussion of problems with equality constraints, as we did for unconstrained problems, let us summarize our findings in a “cookbook recipe” to follow when confronted with specific applications.
Starting Point. Consider a problem
![]()
and suppose that ![]() and
and ![]() are sufficiently smooth, i.e.
are sufficiently smooth, i.e. ![]() where
where ![]() supp
supp![]() and
and ![]() . This ensures that both our first and second order conditions are applicable. If there are points of non-differentiability, they have to considered as border solution points separately.
. This ensures that both our first and second order conditions are applicable. If there are points of non-differentiability, they have to considered as border solution points separately.
Analytical Steps.
For the last step, for economic applications, it is oftentimes helpful to recall that the budget set, and sets defined in a very similar way, are compact, as are the intersections of a finite number of compact sets (as closedness and boundedness are preserved under finite set intersections). The “solution existence” part can also be taken care of in the first step, however, if you have to rely on a limits argument, it may be helpful to know ![]() for your global extremizer candidate
for your global extremizer candidate ![]() .
.
The logic we employ to solve problems featuring also inequality constraints is the one outlined above: a solution candidate will be required to satisfy the Lagrangian conditions for all equality constraints, and further, for the inequality constraints we will impose (i) feasibility, i.e. being contained in the constraint set for a solution candidate, and (ii) our complementary slackness condition. The result we rely on is the Karush-Kuhn-Tucker theorem that tells us the necessary and sufficient conditions for an optimum. Here, we only state it, as the application procedure is more or less analogous to the “Lagrangian cookbook formula”, and the central take-away from this Chapter should be the general foundation of unconstrained optimization and how we formally/intuitively justify the Lagrangian approach.
For the problem ![]() with only inequality constraints
with only inequality constraints
![]()
where ![]() are all
are all ![]() functions, the result may be summarized as follows:
functions, the result may be summarized as follows:
Theorem: Karush-Kuhn-Tucker Theorem.
For ![]() , consider the optimality conditions
, consider the optimality conditions
Then,
In contrast to the Lagrange Theorem discussed earlier, what has changed in the Karush-Kuhn-Tucker (KKT) Theorem is that the rank condition has yet become more complex again. Intuitively, when varying candidates ![]() , the set of “relevant” equality constraints changes because at different
, the set of “relevant” equality constraints changes because at different ![]() , different
, different ![]() will hold with equality. In consequence, we have a different rank condition at different
will hold with equality. In consequence, we have a different rank condition at different ![]() , expressed by the more unwieldy characterization above. Nonetheless, the concept is the same as before, and as there, we must separately identify singularity candidates from points that violate this condition, if there are any. The rest of the “necessity” part of the theorem follows the logic discussed earlier: points must be feasible, and either an inequality constraint holds with equality
, expressed by the more unwieldy characterization above. Nonetheless, the concept is the same as before, and as there, we must separately identify singularity candidates from points that violate this condition, if there are any. The rest of the “necessity” part of the theorem follows the logic discussed earlier: points must be feasible, and either an inequality constraint holds with equality ![]() , or it does not constrain our ability to maximize
, or it does not constrain our ability to maximize ![]() , i.e. the value of the objective function, locally
, i.e. the value of the objective function, locally ![]() , which we summarize in the complementary slackness condition.
, which we summarize in the complementary slackness condition.
The “sufficiency” part of the theorem summarizes the key insights from the issue of “convex optimization”. Deriving this result is beyond the scope of this class. However, note that when all conditions are met, that is, the linear independence rank condition (also called constraint qualification), the shape criteria for objective and constraint functions and ![]() (also called Slater’s condition) are all satisfied, then the optimality conditions are indeed equivalent to the local maximizer property, which greatly simplifies the search for local extremizers. Furthermore, note that for search of local minimizers, the conditions are exactly the same, with the exception that
(also called Slater’s condition) are all satisfied, then the optimality conditions are indeed equivalent to the local maximizer property, which greatly simplifies the search for local extremizers. Furthermore, note that for search of local minimizers, the conditions are exactly the same, with the exception that ![]() must be convex rather than concave to obtain sufficiency.
must be convex rather than concave to obtain sufficiency.
As you may have noted, thus far, we have not addressed problems with both equality and inequality constraints, which are, however, very relevant to economics – for instance, you can think of any equality-constrained problem with added non-negativity constraints for some choice variables. So, what about problems ![]() of the form
of the form
![]()
Here, we also have a variant of KKT:
Theorem: Karush-Kuhn-Tucker with Equality Constraints.
For ![]() and
and ![]() , consider the optimality conditions
, consider the optimality conditions
Then, if ![]() is a local maximizer of the constrained problem for which the set
is a local maximizer of the constrained problem for which the set ![]() is linearly independent, there exist
is linearly independent, there exist ![]() and
and ![]() such that
such that ![]() satisfies the optimality conditions.
satisfies the optimality conditions.
Thus, the “inequality-only” KKT transfers with two caveats: the first is technical and refers to the fact that constraint qualification has become more complex: because all equality constraints always “bind”, i.e., hold with equality, they need to be considered in the linear independence test set. The second is more severe from a methodological point of view: sufficient conditions are no longer “readily” obtained, and for problems with both equality and inequality constraints, we usually only use necessary conditions. While this may sound unfortunate, in many applications, it suffices to check for solution existence and then compare the values of candidates that remain after the FOC, which are usually not many.
That being said, it may still be quite tedious — or at least, time-consuming — to apply KKT, and it is also more error-prone relative to the simpler Lagrangian method. Fortunately, in economics, we can frequently avoid KKT by simplifying the problem to an equality-only or entirely unconstrained problem. This shall be the purpose of our remaining discussion.
In the following, let us consider when and how we can re-write seemingly inequality-constrained problems as equality-constrained, which greatly facilitates the analytic solution. To start off, consider again the general constrained maximization problem,
![]()
Instead of solving it using KKT, we may be able to re-write it as
![]()
which we can apply the more familiar and straightforward Lagrangian method to. Generally, there are two approaches to simplifying the problem: (i) imposing that an inequality constraint is binding, i.e. that it necessarily holds with equality (and thus is “not really an inequality constraint at all”), or (ii) dropping inequality constraints.
Let us study these methods in the context of the budget-constrained utility maximization problem we already introduced,
![]()
with price vector ![]() such that
such that ![]() for all
for all ![]() and
and ![]() . Utility functions that we typically consider are such that
. Utility functions that we typically consider are such that ![]() is strictly increasing in all arguments, i.e.
is strictly increasing in all arguments, i.e. ![]() , an assumption that we are usually ready to impose because strictly more is typically strictly better in the view of the consumer. Moreover, we assume that the marginal utility of the first bit is infinitely high, i.e.
, an assumption that we are usually ready to impose because strictly more is typically strictly better in the view of the consumer. Moreover, we assume that the marginal utility of the first bit is infinitely high, i.e. ![]() . Common examples that satisfy these conditions are Cobb-Douglas or Constant Elasticity of Substitution utility functions.
. Common examples that satisfy these conditions are Cobb-Douglas or Constant Elasticity of Substitution utility functions.
The first simplification (“not really an inequality constraint”) can be applied to the budget constraint: a point ![]() with
with ![]() can never be a solution, because the consumer can spend more to increase utility! Thus, all solutions of the initial problem will be solutions of the re-written problem
can never be a solution, because the consumer can spend more to increase utility! Thus, all solutions of the initial problem will be solutions of the re-written problem
![]()
Whenever this condition in bold holds, the simplification is justified. Next, note that the marginal utility from spending money on good ![]() is
is ![]() (because 1 dollar gives
(because 1 dollar gives ![]() units of the good). For any
units of the good). For any ![]() such that
such that ![]() and
and ![]() , we can marginally decrease spending on
, we can marginally decrease spending on ![]() and increase spending on
and increase spending on ![]() – and, by our zero limit assumption for the marginal utility, generate a large leap in utility. Thus, the point
– and, by our zero limit assumption for the marginal utility, generate a large leap in utility. Thus, the point ![]() with
with ![]() can not be an optimum. Thus,
can not be an optimum. Thus, ![]() will never bind, and if
will never bind, and if ![]() solves our problem, it is also a local maximizer in the problem
solves our problem, it is also a local maximizer in the problem
![]()
The Lagrangian approach of this problem gives ![]() , and we can ex-post impose that
, and we can ex-post impose that ![]() , i.e. that all entries in
, i.e. that all entries in ![]() must be non-negative. In case of a bivariate Cobb-Douglas function
must be non-negative. In case of a bivariate Cobb-Douglas function ![]() ,
, ![]() , it may be a good exercise to formally verify that the optimal input ratio
, it may be a good exercise to formally verify that the optimal input ratio ![]() is given by
is given by ![]() , pay special attention to the line of arguments that ensures that this is indeed the unique global maximum. Thus, we can restrict the role of inequality constraints to feasibility of points in the Lagrangian problem, making them a further criterion in the “cookbook recipe” outlined above according to which we may rule out candidates identified from the FOC.
, pay special attention to the line of arguments that ensures that this is indeed the unique global maximum. Thus, we can restrict the role of inequality constraints to feasibility of points in the Lagrangian problem, making them a further criterion in the “cookbook recipe” outlined above according to which we may rule out candidates identified from the FOC.
Accordingly, we may be able to reduce the problem to either a standard Lagrangian problem if we are able to argue that the inequality constraints are actually equality constraints, or solve an equivalent Lagrangian problem with an additional feasibility condition that rules out some of the critical values. Indeed, most optimization problems you face during the Master’s classes that feature inequality constraints can be reduced to such Lagrangian problems that you can solve using the methods discussed above.
As a final note on problem simplification, recall our motivation for deriving our one-equality-constraint procedure from the implicit function theorem: it may not always be possible to represent constraints using global, explicit functions. On the other hand, sometimes, this may indeed be the case. If so, you can always get rid of the respective constraint – solve for the explicit function representing a constraint and plug it into the problem! This usually makes the problem much easier to solve, as you reduce its dimensionality and the number of constraints. As an example, you can consult the elaborations on the explicit function in the section “Level Sets and Implicit Functions for Optimization” that we used to re-write the two-dimensional constrained problem as a one-dimensional, unconstrained one. When applying this trick, be sure to plug the explicit function not only in to the objective, but also to the other constraints, if any.
We have started by formally studying unconstrained optimization problems, which has allowed us to highlight these problems’ key aspects and properties, to formally justify our first-and second order condition solution approach, and to make clear how we may generalize the respective insights to the case where optimization is subject to equality constraints. For notational simplicity, we have proceeded to a rigorous formal study of the problem with one equality constraint, where we outlined necessary and sufficient conditions for interior solutions. Thereafter, we generalized this approach to multiple constraints exploiting the structural similarity of the vector space ![]() to the space of real numbers, and identified a stepwise procedure to solving general equality-constrained problems using the Lagrangian method. Subsequently, we investigated problems that feature inequality constraints (such as budget constraints and non-negativity constraints) and outlined possible approaches to reduce them to standard Lagrangian problems. In case this reduction is not applicable, we may consult the Karush-Kuhn-Tucker conditions. Finally, we saw that when we have an intuitive way of thinking about what “relaxing the constraint” refers to, we can utilize a mathematically simplistic and elegant way to determine the type of an extremizer that avoids computing a large amount of matrices and their determinants. From our discussions in this chapter, it has emerged that thorough understanding of the Lagrangian method and especially the intuition for the Lagrangian multipliers suffices to understand the approach to most economic optimization problems.
to the space of real numbers, and identified a stepwise procedure to solving general equality-constrained problems using the Lagrangian method. Subsequently, we investigated problems that feature inequality constraints (such as budget constraints and non-negativity constraints) and outlined possible approaches to reduce them to standard Lagrangian problems. In case this reduction is not applicable, we may consult the Karush-Kuhn-Tucker conditions. Finally, we saw that when we have an intuitive way of thinking about what “relaxing the constraint” refers to, we can utilize a mathematically simplistic and elegant way to determine the type of an extremizer that avoids computing a large amount of matrices and their determinants. From our discussions in this chapter, it has emerged that thorough understanding of the Lagrangian method and especially the intuition for the Lagrangian multipliers suffices to understand the approach to most economic optimization problems.
To test how well you understood the second half of the discussions on optimization, you can do a short quiz found here.