Chapter 5 – Econometrics – E600 Mathematics

An overview of this chapter’s contents and take-aways can be found here.

The final chapter of this script gives a brief introduction into the realm of econometrics. Put simply, econometrics can be described as the study of methods that allow statistical analysis of economic issues. To understand what we do in econometrics/statistics, we need to introduce some concepts and results from probability theory.

Table of Contents

Probability Space and Probability Measure

Definition: Probability Space.
A probability space $\mathcal P$ is a triple $\mathcal P := (\Omega, \mathcal A , P)$ , where

- $\Omega$ is the sample space, the set of all possible outcomes,
- $\mathcal A$ is the event space, the set of all possible events, and
- $P: \mathcal A \to [0, 1]$ is the probability measure that assigns events $A\in \mathcal A$ a probability.

Probability spaces are best illustrated with a simple example: consider the case of rolling a regular dice. Before the dice is rolled, the set of possible outcomes is $\Omega = \{ 1, 2, 3, 4, 5, 6 \}$ . Examples of events that could occur are a specific number being rolled, e.g. $A = \{ 2 \}$ or that an even number is rolled, $A = \{2, 4, 6\}$ . Generally, any combination of elements in $\Omega$ may constitute an event.

It remains to define the probability measure $P: \mathcal A \to [0, 1]$ that assigns events $A \in \mathcal A$ a probability between 0 and 1. Clearly, the measure should assign $A = \Omega$ , the event that any number between 1 and 6 is rolled, a probability of 1 and conversely, not turning out a number between 1 and 6 should have zero probability. Lastly, thinking about the probability that either a 1 or a 2 is thrown with a fair dice, it is intuitively clear that the probabilities of both events should add up. These three requirements are in fact sufficient to define a probability measure:

Definition: Probability Measure.
Consider a sample space $\Omega$ and an event space $\mathcal A$ . Then, a function $P: \mathcal A \to [0, 1]$ is called a probability measure on $(\Omega, \mathcal A)$ if

- $P(\Omega) = 1$ and $P(\varnothing) = 0$ is the sample space, the set of all possible outcomes,
- if $A, B\in \mathcal A$ are disjoint, i.e. $A \cap B = \varnothing$ , then $P(A \cup B) = P(A) + P(B)$ .

For the second property, the focus on disjoint sets is crucial: if some elements $\omega\in\Omega$ would realize both $A$ and $B$ , for instance modifying $B= \{2,3\}$ , then additivity need not be assumed. Note that by the second property, it is usually sufficient to know the probability of events referring to individual elements of $\Omega$ , as any event $A$ can be decomposed into a disjoint union of such events: $A = \bigcup_{i\in I} \{\omega_i\}$ , $\omega_i \in \Omega$ . For notational simplicity, we define $P(\omega) := P(\{\omega\})$ for $\omega \in \Omega$ .

As an exercise, try to define the probability measure that characterizes rolling a rigged dice for which it is twice as likely to roll a 6 than it is to roll a 1, but all other numbers remain as likely as with a fair dice.

We know that $P(\omega)=1/6$ for any $\omega \in \Omega \backslash\{1,6\}$ , so that $P(1) + P(6) = 2/6$ . By $P(6) = 2 P(1)$ , we get $3P(1) = 2/6$ , or $P(1) = 1/9$ , and $P(6) = 2 P(1) = 2/9$ .

To introduce conditional probabilities intuitively, consider again the example of the regular dice. What is the probability of throwing a 2, given that you already know that the outcome is an even number? Intuitively, it is clear that we now must compare the probability of a 2 against the probability of the subset of even numbers instead of the whole sample space. We formalize this intuition as follows:

Definition: Conditional Probability.
Consider a sample space $\Omega$ and an event space $\mathcal A$ and two events $A, B \in \mathcal A$ with $P(B)>0$ . The conditional probability of $A$ given $B$ is defined as:

$P(A|B):=\frac{P(A\cap B)}{P(B)}$

For the following considerations, the picture below provides helpful intuition. The probability of the union of the two non-disjoint events A and B is given by

$P(A\cup B) = P(A) + P(B)-P(A\cap B)$

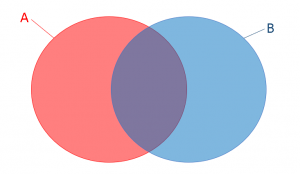
The following result will be very helpful when working with conditional probabilities:

Theorem: Bayes’ Rule.
Consider disjoint sets $\{B_i\}_{i\in\{1,\ldots,n\}}$ where $\cup_{i}B_i = \Omega$ and $P(B_k)>0, k = 1, \hdots, n$ and $A \in \mathcal A:P(A)>0$ . For all $k \in \{1, \hdots n\}$

$P(B_k|A) = \frac{P(A|B_k)P(B_k)}{P(A)} = \frac{P(A|B_k)P(B_k)}{\sum_{i=1}^{n}P(A|B_i)P(B_i)}$

Definition: Independence.
Two events $A, B$ with are set to be stochastically independent if:

$P(A\cap B)=P(A)P(B)$

For all $B$ with $P(B)>0$ , independence implies that $P(A) = P(A|B)$ . As an example for two independent events in our dice example, consider the event of throwing a number strictly smaller than 3, and the event of throwing an odd number. The probability of throwing an odd number is $\frac{1}{2}$ , and and the conditional probability of throwing an odd number given that the number is strictly smaller than 2 is also $\frac{1}{2}$ .

Random Variables and their Distribution

In most practical scenarios, we care less about the realized events themselves, but rather about (numeric) outcomes that they imply. For instance, when you plan on going to the beach, you do not want to know all the meteorological conditions $\omega \in \Omega$ in the space of possible conditions, but you care about the functions $x(\omega) = \mathds 1[\omega \text{ leads to rain}]$ and about $c(\omega)$ that measures the temperature in degrees Celsius implied by the conditions $\omega$ . In other words, you care about two random variables: variables $X$ on the real line that are determined by (possibly much richer) outcomes in the event set $\Omega$ of a probability space.

Definition: Random Variable, Random Vector.
Consider a probability space $(\Omega, \mathcal A , P)$ . Then, a function $x:\Omega \mapsto \mathbb R$ is called a random variable, and a vector $\mathbf x = (x_1,x_2,\ldots, x_n)'$ where $x_i$ , $i\in\{1,\ldots,n\}$ are random variables, is called a random vector.

This definition gives a broad definition of the random variable concept. Those with a stronger background in statistics or econometrics may excuse that it is very vague and simplistic; the concept is mathematically not straightforward to define, and for our purposes, it suffices to focus on the characteristics stated in the definition.

Continuing the example of the fair dice roll, let’s consider a game where I give you 100 Euros if you roll a 6, but you get nothing otherwise. Can you define the function $\pi(\omega)$ that describes your profit from this game, assuming for now I let you play for free?

The function is $\pi: \{1,\ldots, 6\}\mapsto\mathbb R$ , $\omega \mapsto \pi(\omega)$ with $\pi(\omega) = 0$ for $\omega \in \{1,2,3,4,5\}$ and $\pi(\omega) = 100$ for $\omega = 6$ .

A key concept related to random variables $X$ is their distribution, i.e. the description of probabilities characterizing the possible realizations of $X$ . Our leading example of the dice roll, and the game where you can win 100 Euros, is an example of a discrete random variable, characterized by a discrete probability distribution. For such random variables, there are a finite number of realizations (in our case: two, either 0 Euros or 100 Euros), and every realization may occur with a strictly positive probability (5/6 vs. 1/6).

The other case is a continuous probability distribution, with an infinite number of realizations that can not be attributed positive probability: $P(X = x) = 0$ for any $x\in\mathbb R$ . Probably the most famous example of a continuous distribution is the normal distribution. As an example consider the average weight of a package of cornflakes. The machine filling the packages aims for a certain weight, but getting a package with exactly this weight has probability zero. If you have a very large number of cornflakes packages and stack packages with weights in a given interval, ordering these intervals from the smallest to the largest, you will get a curve that looks somewhat like a discretized version of the curve below. We call this curve density, and the integral of the density the distribution of the random variable. The density of a normal random variable is given as $f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2}}exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$ . Below, you can see a plot of a normal random variable with mean $\mu = 0$ and standard deviation $\sigma = 1$ . We call this a standard normal random variable.

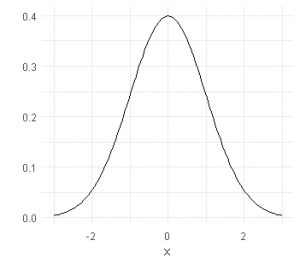
Often, we characterize the distribution with it’s cumulative distribution function as $P(X\leq a) = F(a) = \int_{-\infty}^{a} f_X(x) dx$ , in our case $F(a) = \int_{-\infty}^{a} \frac{1}{\sqrt{2\pi \sigma^2}}exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) dx$ .

The probability density function we have seen above is the derivative of this function: $f_X(a) = F_X'(a)$ .

Using the distribution of a random variable, we can now define its moments: the so-called p-th moment of the distribution is given as $\int_{-\infty}^{\infty} x^{p} f_X(x) dx$ . The first moment of a distribution is called it’s expected value.

Definition: Expected Value.
Consider a probability space $(\Omega, \mathcal A , P)$ and a random variable $X:\Omega \mapsto \mathbb R$ on this space, with probability density function $f_X$ . Then, the expected value $\mathbb E[X]$ of $X$ is defined as the following integral

$\mathbb E[X] = \int_{-\infty}^{\infty} x f_X(x) dx,$

and for a transformation $g(X)$ of $X$ ,

$\mathbb E[g(X)] = \int_{-\infty}^{\infty} g(x) f_X(x) dx.$

Definition: Variance, Standard Deviation.
Consider a probability space $(\Omega, \mathcal A , P)$ and a random variable $X:\Omega \mapsto \mathbb R$ on this space. Then, the variance of $X$ is defined as $Var[X] = \mathbb E[(X- \mathbb E[X])^2]$ , and its square root is called the standard deviation of $X$ , denoted $sd(X) = \sqrt{Var[X]}$ .

The expected value for discrete distributions, when $\{x_i\}_{i\in I}$ is the set of values that $X$ can take with positive probability, simplifies to $\mathbb E[X] = \sum_{i\in I} P(X=x_i) \cdot x_i$ . This shows the intuition: you expect the value $x_i$ with probability $p_i = P(X=x_i)$ , and you expectation is then simply the sum of all these terms.

Random Vectors

All concepts considered so far could be developed on the basis of univariate random variables, but work similarly for random vectors, i.e., multiple random variables. Next, we are going to introduce concepts for more than one random variable.

Definition: Covariance, Correlation.

- For two random variables $X$ and $Y$ , the covariance is defined as
  $Cov(X,Y) := \mathbb{E}\left(\left(X-\mathbb{E}(X)\right)\left(Y - \mathbb{E}(Y)\right)\right)$
- If additionally $V(X), V(Y)\geq 0$ , we can define the correlation as
  $\rho(X,Y):=\frac{Cov(X,Y)}{\sqrt{V(X)V(Y)}}$

If $Cov(X,Y) = 0$ , X and Y are called uncorrelated. To further characterize how X and Y behave jointly, we can define their joint distribution. For brevity, we are again confining ourselves to the special cases of jointly discrete and jointly continuous random variables.

Definition: Joint Distribution.

- For two random variables that are jointly continuously distributed, with density $\phi_{X,Y}$ , we define their joint distribution as the probabilty measure mapping from sets $B \in \mathcal{B\times B}$ to $[0,\infty]$ as
  $P_{X\times Y} = \int_B \phi_{X,Y}(x,y)dxdy$
- For two random variables that are jointly discretely distributed, we define their joint distribution as
  $\sum_{k,l = 1}^{\infty}P(X = x_k,Y = y_l)\mathbf{1}(X = x_k,Y = y_l)$

As a sidenote: defining the joint distribution as a function mapping from $B \times B$ to $[0, \infty]$ is not formally correct. Instead of $B \times B$ , the domain of the pobability measure is the Borel-set over $\mathbb{R}^2$ . The wrong “definition” above was chosen to make the definition of marginal distributions more intuitive.

Definition: Marginal Distribution, Marginal Density.
Given two jointly continously distributed random variables $X$ and $Y$ , the marginal distribution of X is defined as

$P_X(B) = \int_{B \times \mathbb{R}} \phi_{X,Y}(x,y) dy \: dx = \int_B\left(\int_{\mathbb{R}}\phi_{X,Y}(x,y)dy\right)dx\\ =\int_B\phi_X(x)dx$

where $\phi_{X}(x)$ is called the marginal density of $X$ .

Going from joint to marginal densities is pretty simple, as you have seen in the definition above: one “integrates out” the random variable that one is not interested in. Remeber that given Fubini’s Theorem, the order of integration does not matter (at least for most cases we consider in economics). Thus, we can get marginal distributions for both $X$ and $Y$ .

We can now translate the concept of independence to random variables:

Definition: Independence of Random Variables.
Two random variables $X$ and $Y$ are independent if, for any two sets of real numbers $A$ and $B$

$P(X\in A, Y \in B) = P(X \in A)P(Y \in B)$

In other words, X and Y are indepented if, for all A and B, the events $E_A = \{X \in A\}$ and $E_B =\{Y \in B\}$ are independent.

The independence of two random variables has important implications for their joint cumulative distribution function:

$\forall a,b \in \mathbb{R}: P(X\leq a, Y \leq b) = P(X \leq a)P(Y \leq b)$

which has the following implication for the joint density of jointly discrete random variables:

$p_{X,Y}(x,y) = p_X(x) p_Y(y) \forall x, y$

and for jointly continuous random variables

$f_{X,Y}(x,y) = f_X(x) f_Y(y) \forall x, y$

In words, two random variables X and Y are independent if knowing the value of one does not change the distribuion of the other. Their joint density is thus simply the product of the marginal densities. This has important implications, some of which affect the way we can work with expectations, variances and covariances:

Theorem: Rules for Expected Values, Variances and Covariances.
Let $X,Y,Z$ be random variables, $\alpha, \beta$ be scalars, $f,g$ functions, then:

Expected Values:

(Linearity) $\mathbb{E}(\alpha X + \beta Z) =\alpha \mathbb{E}(X) + \beta \mathbb{E}(Z)$
(Products of Intependent RV) if $X,Y$ are independent $\implies \mathbb{E}(XY) = \mathbb{E}(X)\mathbb{E}(Y)$
(Jensens Inequality) for a convex function f, $\mathbb{E}(f(X)) \geq f(\mathbb{E}(X))$
for a concave function g $\mathbb{E}(g(X)) \leq g(\mathbb{E}(X))$

Variances:

$Var(X)\geq 0$ and $Var(X)=0 \iff \exists \alpha: P(X = \alpha)=1$
$Var(X)= \mathbb{E}((x-\mathbb{E}(X))^2) = \mathbb{E}(X^2)-\mathbb{E}(X)^2$
$Var(\alpha X + \beta) = \alpha^2 Var(X)$
if $X,Y$ independent $\implies Var(X+Y) = Var(X) + Var(Y)$

Covariances:

(Symmetry) $Cov(X,Y) = Cov(Y,X)$
$Cov(\alpha X,Y) = \alpha Cov(X,Y)$ and $Cov(\alpha X, \beta Y) = \alpha \beta Cov(X,Y)$
$Cov(X+Y,Z) = Cov(X,Z)+Cov(Y,Z)$
$Cov(X, \alpha) = 0$
Note that $Cov(X,X) = Var(X)$
if $X,Y$ independent $\implies Cov(X,Y) = 0$

As an exercise, try to prove the rules for variances and covariances using the rules established for expected values.

If you feel like testing your understanding of the discussion thus far, you can take a short quiz found here.

Conditional Expectations

Having introduced joint and marginal distributions of random variables, we now introduce the conditional expectation function. We first focus on the simpler case of two jointly discrete random variables. We can write the probability mass function for X given $Y = y$ , given $P(Y = y) > 0$ as

$p_{X|Y}(x|y) = P(X = x|Y = y) = \frac{p_{X,Y}(x,y)}{p_Y(y)}$

For a given value of Y, we can thus define $\mathbb{E}(X|Y = y)$ for all values y such that $P(Y = y)>0$ as

$\mathbb{E}(X|Y = y):=\sum_x x P (X= x|Y = y)\\ =\sum_x x p_{X|Y}(x|y)$

In this course, we will leave out the more technical definitions of conditional expectations and simply note that for jointly continuous random variables, things work similarly. The twist is that the probability mass function of $Y = y$ will be zero for any value y for a continuous random variable. Thus, we must work with joint and marginal density functions instead, to define the conditional density as:

$f_{X|Y}(x|y) = \frac{f_{X,Y}(x,y)}{f_Y(y)}$

and the conditional expectation for $X$ given $Y = y$ with $f_Y(y)$ as

$\mathbb{E}(X|Y = y):=\int_{-\infty}^{\infty} x f_{X|Y}(x|y)dx\\ =\sum_x x p_{X|Y}(x|y)$

Typically, we are interested in the conditional expectation $\mathbb{E}(X|Y = y)$ for the whole distribution of $Y$ , and not just at a single value $Y = y$ . To characterize the conditional expectation for all values $y$ for which $f_Y(y)>0$ , we consider the conditional expectation as a function mapping from the support of Y to the $\mathbb R^n$ :

Definition: Conditional Expectation.
The conditional expectation function $\mathbb{E}(X|Y)$ is a function g with

$g: \{y \in support(Y): f_y(y)>0\}\rightarrow \mathbb{R}^n.$

This definition is imprecise, but the formal definition of the conditional expectation function is unintuitive, and thus left out of this course.

In econometrics, you will work a lot with conditional expectations, so it is useful to familiarize ourselves with some rules and properties:

Theorem: Rules for Conditional Expectations.
Let $X,Y,Z$ be random variables, $\alpha, \beta$ be scalars, $f$ a function then:

(Linearity) $\mathbb{E}(\alpha X + \beta Z|Y) =\alpha \mathbb{E}(X|Y) + \beta \mathbb{E}(Z|Y)$
(Law of Iterated Expectations) $\mathbb{E}(\mathbb{E}(X|Y)) = \mathbb{E}(X)$
$\mathbb{E}(f(y)X|Y)= f(Y)\mathbb{E}(X|Y)$
(Tower) $\mathbb{E}(\mathbb{E}(X|Y)|Y) = \mathbb{E}(X|Y)$
if $X,Y$ independent $\implies \mathbb{E}(X|Y) = \mathbb{E}(X)$

Convergence and Limit Theorems

Before moving on to two central results, we need to define some convergence concepts for random variables:

Definition: Convergence in Probabiltiy.
A series of random variables $(X_n, n \in \mathbb{N})$ converges in probability to some random variable $X$ , if $\forall \epsilon > 0$ :

${\lim}_{n \rightarrow \infty}P\left(|X_n-X|>\epsilon\right) = 0$

Equivalently, we write $X_n \xrightarrow{p}X$ or $plim(X_n) = X$ .

Definition: Convergence in Distribution.
A series of random variables $(X_n, n \in \mathbb{N})$ converges in distribution to some random variable $X$ , if and only if for the cumulative distribution functions, the following holds

${\lim}_{n \rightarrow \infty} F_{X_n}(x) = F_X(x)$

for all $x$ at which $F_X$ is continuous. Equivalently, we write $X_n \xrightarrow{d}X$ .

To put it more simply, $X_n$ converges to $X$ in probability if for large $n$ , $X_n$ and $X$ are as good as equal (deviation smaller than an arbitrarily small $\varepsilon$ ) with probability 1. The fairly abstract definition of convergence in distribution has a relatively simple interpretation: the sequence of distribution functions $F_{X_n}$ associated with the sequence $X_n$ of random variables approaches the distribution function $F_X$ of $X$ pointwise, i.e. at any given location $x$ (this criterion is indeed weaker than the one of uniform convergence, where we would require convergence across locations $x$ ). In simpler words, if $n$ is large enough, then the distribution of $X_n$ should be as good as identical to the one of $X$ . Note that in distinction to convergence in probability, specific realizations of $X_n$ can still be very different from those of $X$ , but their probability distributions will coincide. Therefore, this concept is weaker than convergence in probability.

Using these convergence concepts, we can now introduce the Weak Law of Large Numbers and the Central Limit Theorem:

Theorem: Weak law of large numbers.
Consider a set $\{T_i\}_{i\in\{1,\ldots,n\}}$ of $n$ independently and identically distributed variables with $\mathbb E[T_i^2] < \infty$ . Then,

$\bar T_n := \frac{1}{n} \sum_{i=1}^n T_i \overset p \to \mathbb E[T_i].$

In words,the WLLN tells us that the average of independent random variables that have the same distribution will converge to the expected value of the distribution. This result moves us from theoretical considerations into the world of economics! Suppose we have a large but finite sample of observations of, e.g., household incomes. Using the law of large numbers, we now have an estimator for the expected value of the household income in our population that we can infer from an incomplete subset of this population. The next result is even more powerful:

Theorem: Central limit theorem.
Consider a set $\{T_i\}_{i\in\{1,\ldots,n\}}$ of $n$ independently and identically distributed variables with $\mathbb E[T_i^4] < \infty$ . Then, for $\bar T_n := \frac{1}{n} \sum_{i=1}^n T_i$ , it holds that

$\sqrt{n}(\bar T_n - \mathbb E[T_i]) \overset d \to N(0, Var[T_i]).$

In words, we know that the average of iid random variables is a random variable itself, and we know that this random variable converges in distribution to a normal random variable with the same expected value as each random variable in the sequence $X_n$ and a variance that is equal to the variance of the sequence divided by $n$ , the size of the sample. This result is very general and holds for sequences of random variables almost regardless of their distribution. This result explains the prominence of normal distributions in statistics and will be invaluable for econometrics. While the sample average gives you a good prediction for the expected value of a random variable $X$ , it is silent on how good this prediction is. To assess how precise this prediction is, we can apply the CLT and use the variance to measure the degree of expected deviation of the mean from the expected value. As the variance is based on a square term, we usually re-normalize it by taking the square root when talking about deviations from the expected value, which we call the standard deviation $\sigma$ .

You may test your understanding of the concepts thus far by answering two questions: First, if you were neutral to risk (i.e., you only care about your expected profit), would you play the game where you can win 100 Euros if you roll a 6 if you needed to buy in for 15 Euros (also think about whether you would spontaneously agree to this game without doing the math)? And second, what game do you prefer in terms of expectations, the one where you get a 100 Euros for a 6, or the one where you get $D \cdot X$ Euros, and $X$ is drawn randomly from $[0,25]$ ? And which of these games has the more certain/less volatile outcome? For the latter game, you may use that the dice role is independent of the randomly drawn number $X$ , so that $E[D^kX^k]=E[D^k]E[X^k]$ for any $k\in \mathbb N$ . (If you get stuck, feel free to open and read through the solution.)

The expected value of game 1 is

$\mathbb E[\pi] = \sum_{i\in I} P(X=x_i) \cdot x_i = \frac{5}{6} \cdot 0 + \frac{1}{6} \cdot 100 = \frac{100}{6} \approx 16.67.$

So you should want to pay no more than 16.67 Euros to play this game. If I offer this to you for a buy-in of 15 Euros, if you are risk-neutral, you should do it.

On a side note, in practice, most people would probably not take this game for 15 Euros, as people are risk-averse (they don’t assess games based on expected values) and they dislike losses more than they like gains. Behavioral economists argue that with these conditions, it is rational for people not to play such a game. Things were to change only if we played this game repeatedly, say a 1000 times, where you would expect to eventually be close to the expected profit on average. This is indeed a central result of probability theory, the law of large numbers, as introduced later: $P(|\frac{1}{n}\sum_{i=1}^n X_i - E[X_i]|>\varepsilon) \to 0$ as $n\to\infty$ for any fixed $\varepsilon > 0$ , if the realizations of $X_i$ are independent and follow the same distribution (independent and identically distributed, i.i.d.). Verbally, by repeating a game/an experiment often enough, the average of realizations approaches the expected value with arbitrary precision.

For game 2, the expected value is

$\begin{split} \mathbb E[D\cdot X] = \mathbb E[D] \mathbb E[X] &= 3.5 \cdot \int_{-\infty}^{\infty} x \mathds 1 [x\in[0,25]] \cdot \frac{1}{25} dx \\ &= 3.5 \cdot \frac{1}{25} \int_{0}^{25} x dx \\ & =3.5 \cdot \frac{1}{25} [\frac{1}{2}x^2]_{x=0}^{x=25} \\ &= 3.5 \cdot \frac{625}{50} = 3.5 \cdot 12.5 = 43.75 \end{split}$

Therefore, this game is much preferable to game 1 in terms of the expected profit. To address the volatility of outcomes, we need to compute the variance. Since $Var[X] = E[X^2] - E[X]^2$ , it remains to compute the expectations of the squared terms. First, for game 1,

$\mathbb E[\pi^2] = \sum_{i\in I} P(X=x_i) \cdot x_i^2 = \frac{5}{6} \cdot 0 + \frac{1}{6} \cdot 100^2 = \frac{10000}{6},$

so that

$Var[\pi] = \mathbb E[\pi^2] - \mathbb E[\pi]^2 = \frac{10000}{6} - \left ( \frac{100}{6}\right )^2 = 10 000 \left (\frac{1}{6} - \frac{1}{36}\right ) = \frac{10 000 \cdot 5}{36} \approx 1388.89$

with $sd(\pi) = \sqrt{ 1388.89} \approx 37.27$ .

Next,

$\mathbb E [D^2] = \sum_{d=1}^6 P(D=d) \cdot d^2 = 1/6 (1 + 4 + 9 + 16 + 25 + 36) = 91/6$

and in analogy to above,

$\mathbb E[X^2] = \int_{-\infty}^{\infty} x^2 \mathds 1 [x\in[0,25]] \cdot \frac{1}{25} dx = \frac{1}{25} [\frac{1}{3}x^3]_{x=0}^{x=25} = \frac{25^3}{75} = \frac{625}{3}$

so that

$Var(DX) = \mathbb E [D^2]\mathbb E[X^2] - \mathbb E[D\cdot X]^2 = \frac{91}{6} \frac{625}{3} - \left (43.75\right )^2 \approx 1245.66$

with $sd(DX) = \sqrt{1245.66} \approx 35.29$ .

Therefore, not only is game 2 better in terms of the expected value, but it is also slightly less uncertain/volatile. The more risk-averse an agent is, the more they value certainty, and the uncertainty comparison could therefore be an additional practical reason to opt for game 2 rather than game 1.

Linear Regression Model

Having laid the foundation of stochastic concepts, this final section proceeds to discuss Ordinary Least Squares Regressions (OLS) as the most basic econometric model used in practice. OLS models aim to do the first step from correlations to causality by allowing to “control”/”hold constant” third confounding variables.

Specification

Suppose we set out to come up with a model that allows to assess how a random variable $X$ affects another random variable $Y$ . Suppose that we want to use this model to make predictions about Y in the future, where we do not know the realizations of Y, but we do know realizations of X. Given our prior knowledge about X, we can use the conditional expectation function to re-write Y as

$Y = \mathbb E[Y|X] + e$

where $e$ is the difference between the realized values of Y and its conditional expectation given X. We know that generally, $\mathbb E[Y|X] = g(X)$ is an unknown function $g(\cdot)$ . Moving forward, we can assume that the conditional expectation is linear. If you are unwilling to assume that the CEF is linear, note that by Taylor’s theorem we can approximate the function $g$ using polynomial functions of order p. The simplest such approximation is a linear function, i.e. a polynomial of order 1. This gives another justification for a linear specification of $g(X) = \beta X$ . Under this specification, the equation becomes

$Y = \beta X + e$

In this model, if we observe that $X$ changes by $\Delta X > 0$ units, we expect $Y$ to change by $\beta \cdot \Delta X$ units. Note that this does not assert anything about causality: a non-zero coefficient vector $\beta$ simply tells us that $X$ is useful in predicting $Y$ . To move closer to a causal interpretation, let us consider an additional random vector $Z$ of length $k$ that may describe an indirect relationship between $X$ and $Y$ . Similar to before, we can write

$Y = \mathbb E [ Y | X, Z] + e \overset{\text{Ass. of linearity}}= \beta \cdot (X, Z) + e = \beta^x X + \beta^z Z + e$

Then, $\beta^x$ measures the predictive potential of $X$ for $Y$ conditional on $Z$ , i.e. holding constant $Z$ . This is what we call the ceteris paribus assumption: we hold all other important factors constant and measure the marginal effect of $X$ on $Y$ . To see that $\beta^x$ measures the marginal effect of $X$ on $Y$ , consider the partial derivative

$\frac{\partial Y}{\partial x} = \frac{\partial (\beta_0 + \beta^x x + \beta^z_1 z_1 + \ldots + \beta^z_k z_k + e)}{\partial x} = \beta^x.$

By the linear nature of the model, the levels at which these variables are held constant do not affect the marginal effect of $X$ on $Y$ .

Estimation

Let us proceed with $X$ by further characterizing X as a random matrix of the following form:

$\mathbf X = \begin{pmatrix} 1 & x_{11} & \hdots & x_{1n} \\ 1 & x_{21} & \hdots & x_{2n}\\ \vdots & \vdots \\ 1 & x_{k1} & \hdots & x_{kn} \end{pmatrix}$

X is the data matrix for the equation’s right hand side (RHS) that stacks the observations of the row vector $X_i$ of covariates $j = 1, \hdots k$ for each individual $i = 1, \hdots n$ in its rows . To make sure that you understand the structure of this matrix, think about how it would look like if you had the a simple model with $k=1$ , i.e. only one control variable $X_1 = X$ .

The matrix with one control variable is

$\mathbf X = \begin{pmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{pmatrix}$

where $\{X_i\}_{i\in I}$ are the observations for the random variable $X$ . The vector $\beta$ would in this case be $\beta = (\beta_0,\beta_1)'$ .

We can describe the relationship of interest as

(1) $\begin{equation*} Y = \beta X + e. \end{equation*}$

Now that we have an explicit formula that we intend to use for predicting Y, the question how to best estimate that formula arises. As per the economist’s preference for the Euclidean space (recall that the Euclidean norm captures the direct distance), it seems natural to minimize the distance of the vectors $y = (y_1, \ldots, y_n)'\in\mathbb R^n$ of data points for $Y$ and $\mathbf X \beta$ .

We express the optimization problem minimizing the euclidean distance between $y$ and the (approximation to the) conditional expectation function given $X$ as:

$\min_{b\in \mathbb{R}^2} \| y - \mathbf{X} b \|_2 \hspace{0.5cm}\\ \text{or}\hspace{0.5cm} \min_{b\in \mathbb{R}^2}\sqrt{\sum_{i=1}^n (y_i - b_0 - b_1 x_{i1}- \hdots - b_k x_{ik})^2 }$

Solving this should be a relatively simple task: there are no constraints, and the objective function entails a polynomial of the solution. Note that the square root as a monotonic transformation does not matter for the location of the extrema. Thus, we can solve the equivalent problem

(2) $\begin{equation*} \min_{b\in \mathbb{R}^2}\sum_{i=1}^n (y_i - b_0 - b_1 x_{i1}- \hdots - b_k x_{ik})^2 = \min_{b\in \mathbb{R}^2} \sum_{i=1}^n \hat{e_i}^2 \end{equation*}$

This formulation gives the most common estimators of the linear model their name: least-squares estimators. Note that
$y_i - b_0 - b_1 x_{i1}- \hdots - b_k x_{ik} =: \hat e_i(b)$ is the error in predicting $y_i$ using $X_i$ , which we also call the residual. Therefore, the solution $\hat\beta = \arg\min_{b\in\mathbb R^2} \sum_{i=1}^n (y_i - b_0 - b_1 x_{i1}- \hdots - b_k x_{ik})^2$ , provided that it exists, minimizes the residual sum of squares $RSS(b) = \sum_{i=1}^n \hat e_i(b)^2$ , i.e. the sum of squared prediction errors.

We are now set up to derive the (hopefully unique) solution for the estimator $\hat\beta = \arg\min_{b\in\mathbb R^2} \sum_{i=1}^n \hat e_i(b)^2$ . To test your understanding of Chapter 4, you can try to derive it yourself before reading on. To help you get started, things remain more tractable if you stick with the vector notation, and start from the problem

$\min_{b\in\mathbb R^2} (y - \mathbf X b) ' (y - \mathbf X b).$

If you have tried to solve it, or you want to read on directly, let’s get to the solution of this problem. The first step is to multiply out the objective. Doing so, the problem becomes

$\min_{b\in\mathbb R^2} y'y - y'\mathbf X b - b ' \mathbf X ' y + b ' \mathbf X ' \mathbf X b.$

Taking the following rules for derivatives of vectors and matrices as given, we know that

$\frac{\partial}{\partial b} y'\mathbf X b = y'\mathbf X \hspace{0.5cm}\text{and}\hspace{0.5cm} \frac{\partial}{\partial b} b ' \mathbf X ' \mathbf X b = b' (\mathbf X ' \mathbf X + (\mathbf X ' \mathbf X)') = 2 b' \mathbf X ' \mathbf X .$

Putting these together, the first order condition is

$\mathbf 0' = \frac{\partial}{ \partial b} \left ( y'y - 2 y'\mathbf X b + b ' \mathbf X ' \mathbf X b \right ) = - 2 y'\mathbf X + 2 b' \mathbf X'\mathbf X$

so that the solution $\hat \beta$ must satisfy

$y'\mathbf X = \hat \beta ' \mathbf X'\mathbf X \hspace{0.5cm}\text{or equivalently}\hspace{0.5cm} \mathbf X'\mathbf X \hat \beta = \mathbf X ' y.$

While it looks like we are almost there, there are two things that we need to address: (i) can we invert $\mathbf X'\mathbf X$ to obtain a unique solution? (ii) If we can, does this solution constitute a (strict) local minimum? (And is this local minimum global?)

We know that matrices of the form $A'A$ for $A\in\mathbb R^{n\times m}$ are always positive semi-definite: for $v\in\mathbb R^m$ , $v'A' A v = (Av)' Av = w'w = \sum_{i=1}^m w_i^2 \geq 0$ for $w = Av\in\mathbb R^m$ . Now, recalling Chapter 2, this matrix is indeed positive definite if for any $v\neq\mathbf 0$ , $Av\neq \mathbf 0$ , which is the case if $A$ has full column rank, i.e. no column of $A$ can be written as a linear combination of the remaining columns. If the matrix $\mathbf{X}'\mathbf{X}$ is positive definite, it is invertible.

In models with many RHS variables, the issue of collinearity can be difficult to spot. If you have vectors $x$ and $z$ of observations for random variables $X$ and $Z$ , respectively, then collinearity occurs if $\mathbf 1 = \lambda x + \mu z$ for some $\lambda,\mu \in \mathbb R$ . In practice, statistical software will usually give you an error message if this condition is violated in your data.

Returning to the optimization problem, if the matrix $\mathbf{X}'\mathbf{X}$ is invertible, then the unique solution is

$\hat \beta = (\mathbf X'\mathbf X )^{-1} \mathbf X ' y$

and it constitutes a strict local minimum by positive definiteness of $\mathbf X'\mathbf X$ , the second derivative of the objective function. This local solution is also global, as for any $b\in\mathbb R^2$ , $\lim_{\lambda\to\infty} (y'y - 2 y'\mathbf X (\lambda b) + (\lambda b) ' \mathbf X ' \mathbf X (\lambda b)) = \lim_{\lambda\to\infty} \lambda^2 b' \mathbf X ' \mathbf X b = \infty$ , so that the objective diverges to $+\infty$ in any asymptotic direction.

This solution $\hat \beta = (\mathbf X'\mathbf X )^{-1} \mathbf X ' y$ , called the ordinary least squares (OLS) estimator, can be shown to have very strong theoretical properties: it is unbiased, i.e. $\mathbb E[\hat \beta] = \beta$ , meaning that it is expected to estimate the true parameter $\beta$ , and within the class of all estimators that are unbiased, it has the lowest variance, i.e. it is expected to provide the estimate closest to $\beta$ for any given sample. This estimator always estimates the coefficients of the linear conditional expectations function $\mathbb E[Y|X] = \beta X$ , and even if the conditional expectation function is not linear, the coefficients estimated by the OLS estimator recover the best linear prediction of $Y$ given $X$ . This is a crucial point: when you estimate OLS, you always estimate the best linear prediction, which corresponds to the conditional mean if it can be described by a linear function. Any discussion of “misspecification” or “estimation bias” does (or at least: should!) not argue that we are unable to recover the linear prediction coefficients, but that we are unable to interpret these coefficients in a causal/desired way.

Inference

One thing we have only insufficiently addressed thus far is the quality of estimation. While the OLS estimator is not biased, and it is the “most efficient” estimator (lowest variance among the set of unbiased estimators), in practice, its variance (i.e., the expected squared error) can still be very high – just not as high as the one you would obtain with another estimator. Therefore, if you have a simple model $Y = \beta_0 + \beta^x X + e$ and I tell you that OLS has been applied to obtain $\hat\beta^x = 0.05$ based on 10 data points, would you be confident to preclude that the true value of $\beta^x$ is 0? And would you rule out that it is 1?

To answer such questions, we need to address the uncertainty associated with our estimation. Only once we can quantify this uncertainty we will be able to perform meaningful inference on the estimates we obtained. To do so, we rely on the key concepts of convergence in probability and convergence in distribution established above.

In our context, the random variable will be the OLS estimator $\hat{\beta}$ . Treating the observations $\{(X_i,y_i)\}_{i\in\{1,\ldots,n\}}$ as realizations of $n$ independent and identically distributed random variables $(X_i,Y_i)$ , the OLS estimator is

$\hat \beta = \left (\mathbf X ' \mathbf X \right )^{-1 } (\mathbf X ' y)$

To address the error we make in estimation, it is useful to consider the quantity $\hat \beta - \beta$ . To express it in a useful way, we plug in $y = X\beta + e$ to the expression above, and we obtain

$\begin{split} \hat \beta - \beta &= \left (X' X)^{-1} X'(X \beta + e\right) - \beta \\ & =(X' X)^{-1} X' e \end{split}$

We can represent it using a vector-sum notation over observations $X_i = (1, x_{i1},\hdots x_{ik})$ as (consider the structure of the design matrix $\mathbf X$ to verify that this is true):

$\hat \beta = \left (\frac{1}{n} \sum_{i=1}^n X_i X_i' \right )^{-1 }\frac{1}{n}\sum_{i=1}^n X_i e_i$

This is the quantity that we need to study in order to characterize the error we make in estimating $\beta$ using $\hat\beta$ . To do so, we need to combine the Weak Law of Large Numbers and the Central Limit Theorem with one additional Theorem:

Theorem: Slutsky’s theorem.
Let $\{T_n\}_{n\in\mathbb N}$ and $\{W_n\}_{n\in\mathbb N}$ be sequences of random variables with $T_n\overset d \to N(0, \Sigma)$ and $W_n \overset p \to W$ and $\mathbb E[W^2] < \infty$ . Then,

$W_n T_n \overset d \to N(0, \mathbb E[W]\Sigma \mathbb E[W])$

and if $W_n$ is invertible with probability 1, then also

$W_n^{-1} T_n \overset d \to N(0, \mathbb E[W]^{-1}\Sigma \mathbb E[W]^{-1})$

Theorem: Asymptotic Distribution of the OLS Estimator.
Let $\hat{\beta}$ be the OLS estimator and $\beta$ its expected value. Then,

$\sqrt{n}(\hat{\beta} - \beta) \xrightarrow{d} N(0, \Sigma)$

where $\Sigma$ is the variance matrix of $\hat{\beta}$

Sketch of proof:
Step 0. For OLS, we assume that $\mathbb E[e_i|X_i] = 0$ , which implies that $\mathbb{E}(e_iX_i) =0$ . Using this moment condition, we can derive that $\beta = \mathbb E[ X_i X_i']^{-1}\mathbb E[ X_i Y_i]$ .
Step 1. By the law of large numbers,

$\frac{1}{n} \sum_{i=1}^n X_i X_i' \overset p \to \mathbb E[ X_i X_i'].$

Moreover, the law of large numbers gives

$\frac{1}{n} \sum_{i=1}^n \tilde X_i e_i \overset p \to \mathbb E[\tilde X_i e_i] = \mathbf 0.$

Step 2. Applying the central limit theorem,

$\frac{1}{\sqrt{n}} \sum_{i=1}^n X_i e_i = \sqrt{n} \left ( \frac{1}{n}\sum_{i=1}^n X_i e_i - \underbrace{\mathbb E[ X_i e_i]}_{=0}\right ) \overset d \to N(0, Var[ X_ie_i]).$

The variance of the asymptotic distribution is

$Var[ X_ie_i] = \mathbb E[ X_i X_i ' e_i^2] - \underbrace{\mathbb E[ X_i e_i]\mathbb E[ X_i e_i]'}_{=\mathbf 0} = \mathbb E[ X_i X_i ' e_i^2]$

so that compactly,

$\frac{1}{\sqrt{n}} \sum_{i=1}^n X_i e_i \overset d \to N(0, \mathbb E[ X_i X_i ' e_i^2])$

Step 3. We have two components that correspond to the setup of Slutsky’s theorem. First, putting together the two results of step 1, we obtain the following corollary from Slutsky’s theorem (recalling that convergence in probability to a constant implies convergence in distribution to the same constant):

Corollary: OLS consistency.
For the OLS estimator $\hat\beta = \left (\frac{1}{n} \sum_{i=1}^n \tilde X_i \tilde X_i' \right )^{-1 }\frac{1}{n}\sum_{i=1}^n \tilde X_i Y_i$ , it holds that

$\hat \beta - \beta \overset p \to \mathbb E[\tilde X_i \tilde X_i']^{-1} \mathbb E[\tilde X_i e_i] = \mathbf 0$

and thus also $\hat\beta \overset p \to \beta$ . Therefore, we say that $\hat\beta$ is a consistent estimator of $\beta$ .

This informs us that deviations of $\hat\beta$ from $\beta$ will asymptotically be arbitrarily small with probability 1.

Combining Slutsky’s theorem with the distribution of $\frac{1}{\sqrt{n}}\sum_{i=1}^n \tilde X_i e_i$ obtained above using the CLT, we obtain the distribution of $\sqrt{n}(\hat{\beta}-\beta)$ :

$\sqrt{n}(\hat \beta - \beta) = \left (\underbrace{\frac{1}{n} \sum_{i=1}^n \tilde X_i \tilde X_i'}_{\overset p \to \mathbb E[\tilde X_i \tilde X_i']} \right )^{-1 }\underbrace{\frac{1}{\sqrt{n}}\sum_{i=1}^n \tilde X_i e_i}_{\overset d \to N(0, \mathbb E[\tilde X_i \tilde X_i ' e_i^2])} \hspace{0.5cm}\overset d \to \hspace{0.5cm} N(0, \mathbb E[\tilde X_i \tilde X_i']^{-1} \mathbb E[\tilde X_i \tilde X_i ' e_i^2]\mathbb E[\tilde X_i \tilde X_i']^{-1} )$

We define $\Sigma_{\hat\beta} := \mathbb E[\tilde X_i \tilde X_i']^{-1} \mathbb E[\tilde X_i \tilde X_i ' e_i^2]\mathbb E[\tilde X_i \tilde X_i']^{-1}$ as the asymptotic variance of $\hat\beta$ .
q.e.d.

With this result, for sufficiently large samples, the distribution of $\sqrt{n}(\hat \beta - \beta)$ is approximately equal to the one of a random variable with distribution $N(0, \Sigma_{\hat\beta})$ . This is useful because it also means that

$\hat \beta \overset a \sim N(\beta, \frac{1}{n}\Sigma_{\hat\beta}).$

Here, $\overset a \sim$ is used to indicate that asymptotically, the distribution of $\hat\beta$ can be described as $N(\beta, \frac{1}{n}\Sigma_{\hat\beta})$ . With some oversimplification, for large enough $n$ , the distribution of $\hat\beta$ is as good as indistinguishable from a normal distribution with mean $\beta$ and variance
$\frac{1}{n}\Sigma_{\hat\beta}$ .

The important bit of information obtained from this is that we now have an approximation to the finite sample variance of $\hat \beta$ that is “good” if the sample is “large”. The matrix $\Sigma_{\hat\beta} = \mathbb E[\tilde X_i \tilde X_i']^{-1} \mathbb E[\tilde X_i \tilde X_i ' e_i^2]\mathbb E[\tilde X_i \tilde X_i']^{-1}$ is straightforward to estimate using averages instead of expectations, and replacing the unobserved $e_i$ with its sample counterpart $\hat e_i = Y_i - \tilde X_i ' \hat \beta$ :

$\hat \Sigma_{\hat\beta} = \left (\frac{1}{n}\sum_{i=1}^n \tilde X_i \tilde X_i'\right )^{-1}\frac{1}{n}\sum_{i=1}^n \tilde X_i \tilde X_i' \hat e_i^2 \left (\frac{1}{n}\sum_{i=1}^n \tilde X_i \tilde X_i'\right )^{-1}.$

In the matrix $\frac{1}{n} \hat \Sigma_{\hat\beta}$ , the (1,1) element gives the estimated variance of $\hat\beta_0$ , and the $(2,2)$ element the one of $\hat \beta^x$ , denoted as $\hat\sigma^2_{\beta_0}$ and $\hat\sigma^2_{\beta^x}$ , respectively. One can show that

$\frac{\hat\beta_0 - \beta_0}{\hat\sigma_{\beta_0}} \overset a \sim N(0, 1)\hspace{0.5cm}\text{and}\hspace{0.5cm} \frac{\hat\beta^x - \beta^x}{\hat\sigma_{\beta^x}} \overset a \sim N(0, 1).$

This circumstance can be used to test hypotheses such as “ $\beta^x = 0$ ” or “ $\beta^x = 1$ “.

To conclude the discussion of the linear model, we have introduced the concept of the conditional expectation, and the linear conditional expectation regression model. This model is also useful if the true conditional expectation is not linear, among others due to a Taylor approximation justification. In this model, coefficients can be interpreted as marginal effects of one variable on the outcome $Y$ , holding the other variables constant. Therefore, it allows to describe the partial relationship between $X$ and $Y$ that is unexplained by third variables $Z$ . This model can be estimated using the OLS estimator, which could be derived from a simple unconstrained optimization problem. This estimator has powerful theoretical properties, and always estimates the best linear prediction of $Y$ given $X$ . The practical exercise of the econometrician is usually not to allow for “consistent” estimation of the linear prediction (which is guaranteed), but to write down a linear prediction that is useful for studying a given practical issue at hand. Beyond estimation, we have covered inference, i.e. methods of quantifying estimation uncertainty, as well as their justification through large sample asymptotics. These methods allow to test for, and especially to reject certain values for the estimated parameters in the model.

If you feel like testing your understanding of the latter part of this chapter, you can take a short quiz found here.