Here, you can find a (non-exhaustive!) list of the contents and take-aways of Chapter 3: Multivariate Calculus. This list serves as an opportunity to assess both how thoroughly you should read the chapter before opening it for the first time, and how well you have managed to follow along once you have read it.
Chapter 3: Multivariate Calculus discusses the fundamental concepts of functional analysis in metric spaces, especially spaces of vectors of real numbers, including
-
- invertibility and convexity and concavity
- differentiation: the approach to generalizing arbitrary derivatives from the ones of univariate functions and how multivariate derivatives are defined and how they can be computed
- Taylor approximations, Taylor expansions and total derivatives of multivariate functions
- integration: conceptual basics and rules for computing multivariate integrals
Someone with profound knowledge of the contents of this chapter should
-
- be able to apply the most common operations on functions correctly, including addition, multiplication and composition
- be familiar with terminology related to (possibly) vector-valued functions, and know e.g. the conceptual difference between a multivariate real-valued function and a univariate vector-valued function
- have a graphical intuition for how convexity generalizes from univariate to multivariate functions
- know the concepts of quasi-convexity and quasi-concavity and how to investigate whether a certain function satisfies them
- know the formal definition of a function’s derivative, and how the definition of multivariate derivatives is motivated and generalized from the one of univariate derivatives
- be aware of the three conceptual levels of objects in differential calculus: operators, functions and values
- be familiar with the concepts of the gradient, the Jacobian and the Hessian, and how they are useful for computing multivariate first and second derivatives
- know what a total derivative is and how it can be used to study economic trade-offs and indirect effects of background variables
- be able to investigate multivariate convexity using the second derivative
- be familiar with the definitions of a set’s infimum and supremum
- know how to compute multivariate integrals using Fubini’s Theorem (iterative integration with respect to every dimension)
and be able to answer a number of related questions, including
-
- How do injectivity and surjectivity relate to invertibility? What about bijectivity?
- When and how can a “matrix function” (
 where
where 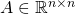 ) be inverted?
) be inverted?
- Which specific differentiability criterion must a function satisfy to be an element of the set
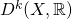 ? What about
? What about 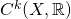 ?
?
- Does a multivariate version of the chain rule for the derivative exist? If so, does the order in which the derivative’s elements are multiplied with each other matter?
- What is the difference between a Taylor expansion and a Taylor approximation? Is either one of these concepts always equal to the underlying function?
- Which mathematical fact justifies the statement “the Taylor approximation for
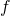 at
at 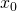 is a good approximation to
is a good approximation to 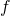 around this point”?
around this point”?
- Is it true that in any metric space
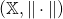 , the norm
, the norm  is continuous? Do you have an intuition for why or why not?
is continuous? Do you have an intuition for why or why not?
- How is the limit
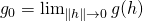 formally defined (
formally defined (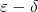 -statement) when the domain of
-statement) when the domain of 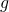 is
is 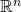 ,
, 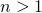 ?
?
- Is it sufficient for differentiability of
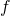 that all partial derivatives of
that all partial derivatives of 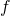 exist?
exist?
- Is every Hessian a Jacobian? Is every Jacobian a Hessian?
- Why is the differential operator not invertible? Explain roughly how the definite integral “solves” this issue.