Here, you can find a (non-exhaustive!) list of the contents and take-aways of Chapter 1: Vector Spaces. This list serves as an opportunity to assess both how thoroughly you should read the chapter before opening it for the first time, and how well you have managed to follow along once you have read it.
Chapter 1: Vector Spaces discusses
-
- how we define a vector space and the intuition of why this is useful
- how to measure mathematical distance using metrics and norms
- set properties in metric and normed spaces: closedness and openness, boundedness and compactness
- the argument for compactness of economic budget sets (with strictly positive prices)
- how to define convergence for general sequences in, and continuity for general functions mapping between metric spaces
Someone with profound knowledge of the contents of this chapter should
-
- be able to think intuitively about objects in vector spaces in terms of direction and magnitude
- know the central building blocks of a vector space definition: set, vector addition and scalar multiplication
- be able to give some examples for common vector spaces economists deal with
- be familiar with key concepts related to vector spaces, including the scalar product and linear independence
- know the definitions of a metric, a norm, and a norm-induced metric
- know that we prefer p-norm-induced metrics for economic applications, and why
- be able to illustrate the intuition of open and closed sets, as well as the concepts of interior, boundary and closure of a set, using a graph of a ball in the
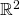
- be familiar with a range of results that facilitate checking set openness and closedness (using e.g. the complement and unions/intersections, or limits of sequences in the set)
- know how to check set boundedness when using a norm-induced metric
- know the definitions of convergence and continuity in metric spaces, and the sequence characterization of continuity
and be able to answer a number of related questions, including
-
- Can you point out two issues of the baseline metric concept that motivate a norm-based approach to the mathematical distance definition?
- How is the Euclidean norm defined? Which p-norm does it correspond to?
- How can you use a norm to assess the length of a vector?
- What’s the natural metric of the
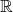 ? How are p-norms a generalization of this natural metric to the
? How are p-norms a generalization of this natural metric to the 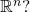
- How can we use interior points, boundary points, and closure points to assess whether a set is open and/or closed?
- Can a set be both open and closed? Can it be neither?
- According to the Heine-Borel Theorem, which two conditions are equivalent to compactness of a subset of the
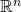 ?
?
- Is a budget set always closed? Under which condition is it compact?